Let ABCD be a square. An arc of a circle with A as centre and AB as radius is drawn inside the square joining the points B and D. Points P on AB, S on AD,Q and R on are taken such that PQRS is a square. Further suppose that PQ and RS are parallel to AC. ThenareaPQRSareaABCD is
18
15
14
25
The correct Answer is:D

Let A(0,0),B(1,0),C(1,1),D(0,1)⇒ Area ABCD = 1
Again let Q(cosα,sinα) & R(cosβ,sinβ)
⇒ coordinate of P(cosα,sinα) & S(cosβ,sinβ)
PQRS is a square ⇒PQ⊥QR⇒ slope of QR=−1= slope of SP
⇒sinβ−sinαcosβ−cosα=−1=sinβ−cosβsinα−cosα
⇒sinβ−sinα=−sinα+cosα
⇒sinβ−cosβ=sinα+cosα.........(i)
and sinα+sinβ=cosα+cosβ...........(ii)
⇒cosα=sinβ
⇒cosα=cos(90−β)
⇒α+β=90∘
Also PQ QR
⇒tanα=12
Area of PQRS=2sin2α=2(15)
Area of PQRSArea of ABCD=2/51=25
Topper's Solved these Questions
- BOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Matematics20videos
KVPY
- BOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part 1 Mathematics45videos
KVPY
- BOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2 MATHMATICS10videos
KVPY
- BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS4videos
KVPY 2021
Similar Questions
Let ABCD be a square. An arc of a circle with A as centre and AB as radius is drawn inside the square joining the points B and D. Points P on AB, S on AD, Q and R on arc BD are taken such that PQRS is a square. Further suppose that PQ and RS are parallel toAC. Then, areaPQRSareaABCD is
View SolutionSide of square ABCD is 7 cm with D as the centre and DA as radius, arc XC is drawn. Find the area of the shaded region with the help of the following flow chart.

 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Plot the points P(1, 0), Q(4,0) and S(1, 3). Find the coordinates of the point R such that PQRS is a square.
A(2,3)B(3,3)C(4,3)D(0,3) - Question 2 - Select One
ABCD is a square of side a. The centre of the circle which circumscribes the square on taking AB and AD as axes is
A(a, -a)B(-a, a)C(1/2,a/2)Dnone - Question 3 - Select One
If a square ABCD is inscribed in a circle of radius 'r' and AB = 4 cm, then the value of r is :
A2 cmB2√2 cmC4 cmD4√2 cm
Draw a circle with centre P. Draw an arc AB of 100∘ measure. Draw tangents to the circle at point A and B.
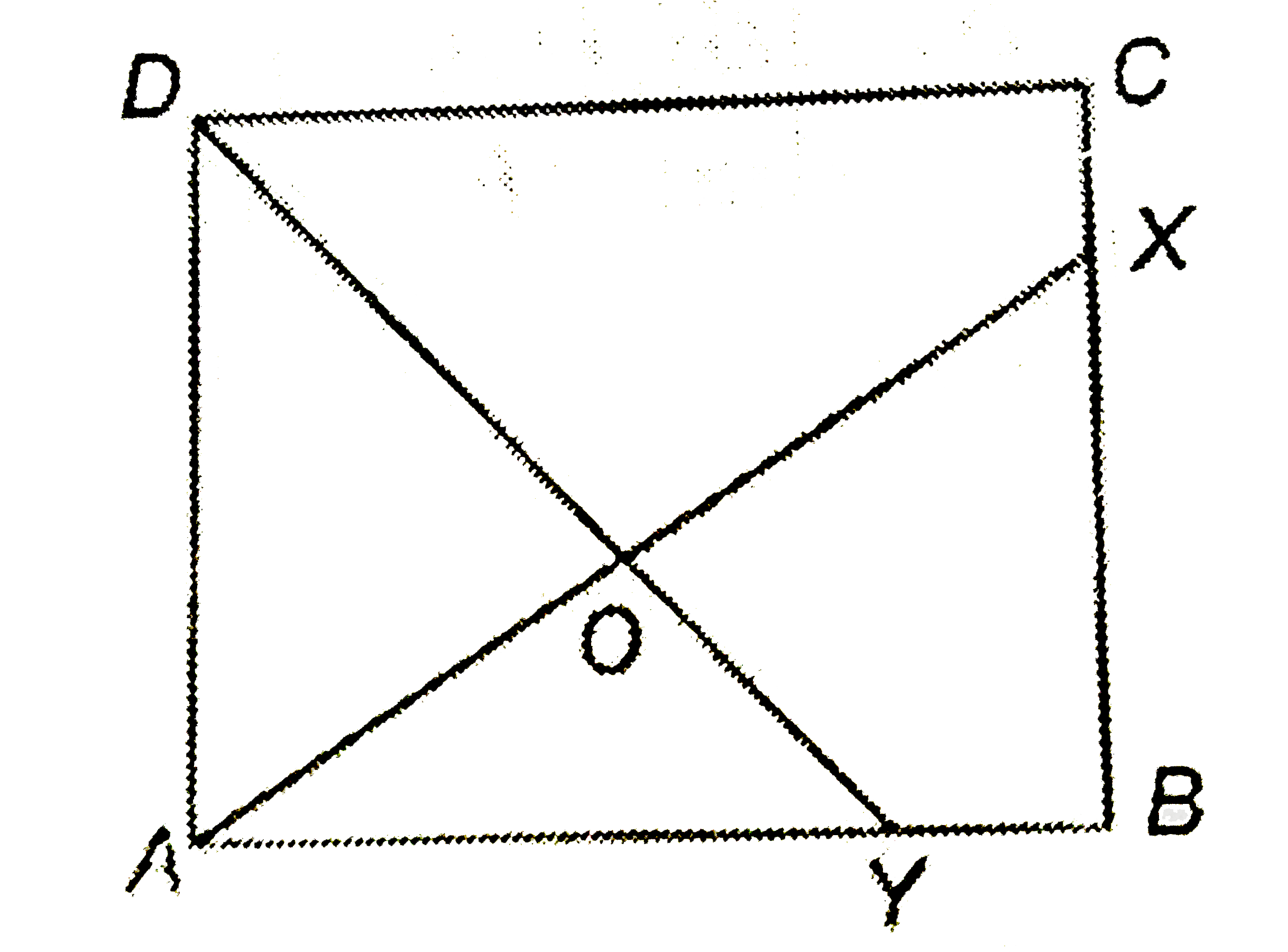
View SolutionIn a square ABCD, A is joined to a point X on BC and D is joined to a point Y on AB. If AX = DY, prove that AX is perpendicular to DY.
 View Solution
View SolutionABCD is a square, A is joined to a point P on BC and D is joined to a point Q on AB. If AP=DQ and AP intersects DQ at R the, ∠DRP is :
View SolutionAC is transverse common tangent to two circles with centres P and Q and radii 6 cm and 3 cm at the point A and C respectively. If AC cuts PQ at the point B and AB= 8cm then the length of PQ is:
View SolutionIn a circle with centre P, AB is a minor arc. Point Ris a point other than A and B on major arc AB. If ∠ARB=80∘, then ∠APB=........
View Solution

