Entropy has great importance in thermodynamics. It is a state function and it is a measure of the degree of disorder or randomness of the system. More is the disorder of the system, greater will be the entropy and vice versa. It is normally expressed in terms of change of entropy.
$(i)$ For a reaction entropy change is given by $Δ S = \sum S (product) - \sum S (reactant)$
$(i i) Δ S = \frac{Q_{r e v}}{T} = \frac{W_{r e v}}{T} = \frac{n R T ln (V_{2} / V_{1})}{T}$
$= n R T \frac{ln (V_{2})}{V_{1}} = n R \frac{ln (P_{1})}{P_{2}}$
$(i i i) Δ S = Δ H - T Δ S$
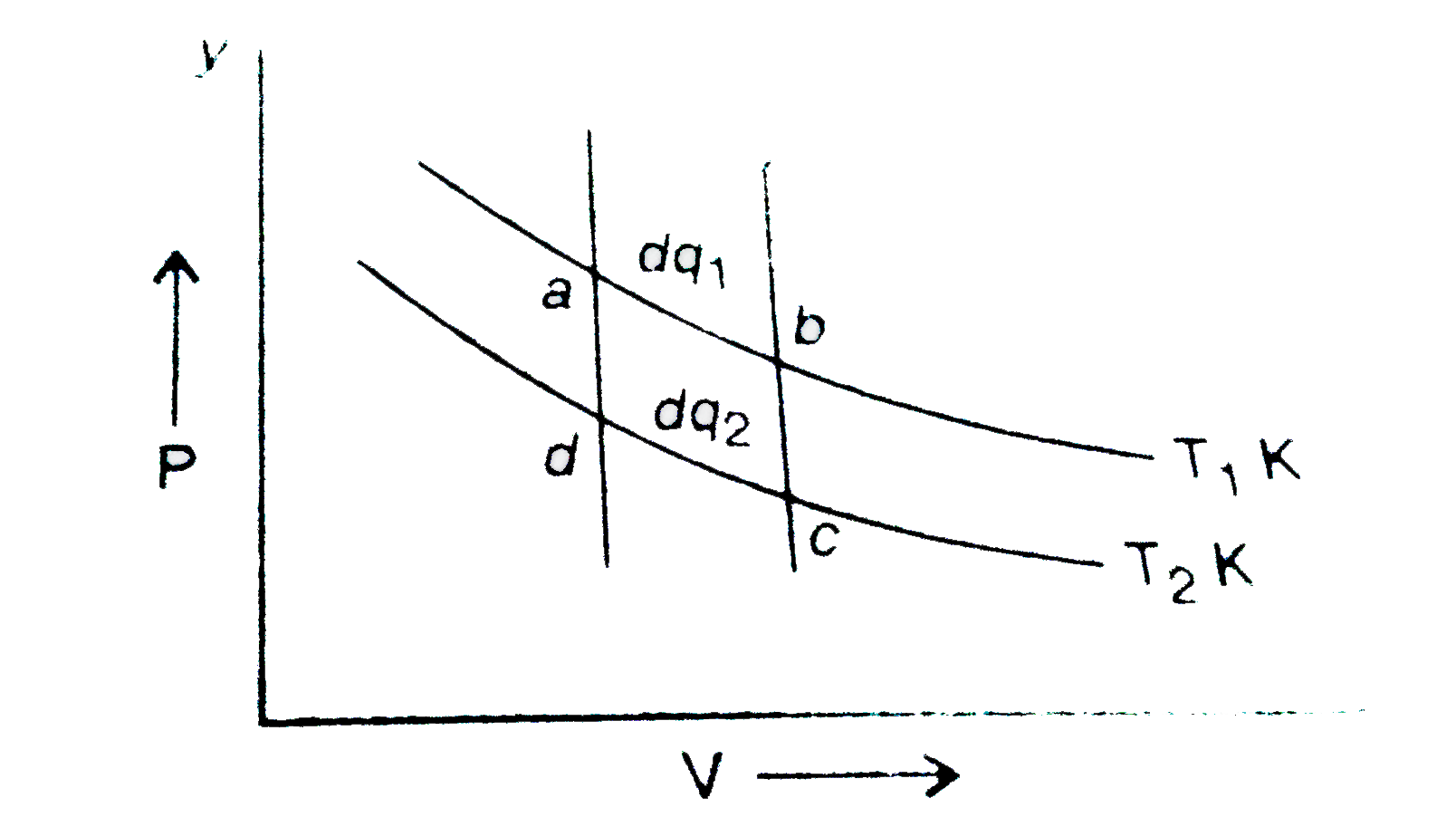
$(i v)$ Entropy change in reversible and irreversible process : Consider a Carnot cycle as shown in figure below in which $a b$ and $c d$ are isothermal.

Irrespective of the path of the system in its reversible change, $d q / T$ is same
For entire Carnot cycle
$\frac{d q_{1}}{T_{1}} - \frac{d q_{2}}{T_{2}} = 0$
$∴ Δ S_{universe} = D e < s S_{system} + Δ S_{surrounding}$
$Δ S_{Surrounding} = \frac{q_{1}}{T_{1}} + \frac{q_{2}}{T_{2}}$ ( $q$ term includes their own sign)
$b c$ and $d a$ are adiabatics. Let $d q_{1}$ be the heat supplied to the working system at $T_{1} K$ and $d q_{2}$ be heat rejected by it to the sink at $T_{2} K$ . All these steps are reversible. In a Carnot cycle.
$\frac{d q_{1} - d q_{2}}{d q_{1}} = \frac{T_{1} - T_{2}}{T_{1}}$ or $\frac{d q_{1}}{T_{1}} = \frac{d q_{2}}{T_{2}}$
Let us now confine our attention only to the change of the system from point $' a'$ to point $' c'$ and attempt to find out the ratio of heat change to the temperature at which thermal changes occur by proceeding from $a$ to $c$ either along $a b c$ or $a d c$ .
Along the path $a b c$ , $\frac{Heat change}{Temp.} = \frac{d q_{1}}{T_{1}}$
Along the path $a d c$ , $\frac{Heat change}{Temp} = \frac{d q_{2}}{T_{2}}$
In case of spontaneous and irreversible expansion to volume $V_{1} + V_{2}$ , $W = 0$ and so will be $Δ U$
In the reversible expansion of the gas at $T K$ from volume $V_{1}$ to $V_{1} + V_{2}$ , heat absorbed $Δ U + R T \frac{ln (V_{1} + V_{2})}{V_{1}}$
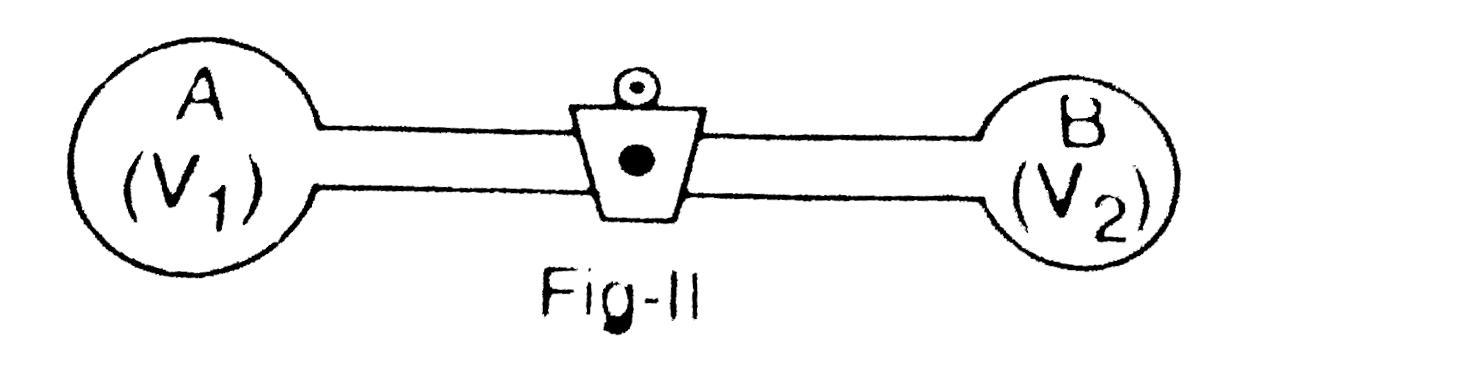
$(v)$ Suppose $n$ moles of an ideal gas are enclosed in a vessel $A$ of volume $V_{1}$ which is connected through a stop cock to a completely evacuated vessel $B$ of volume $V_{2}$ . The system is insulated and has temperature $T K$ .

If the stop cock is opened, the gas will attain the volume $V_{1} + V_{2}$ .
In a reversible isothermal expansion of the gas at $T K$ as shown in figure $I I$ , the $Δ S_{system}$ , $Δ S_{surroundings}$ and $Δ S_{universe}$ will be respectively ?

A

$R \frac{ln (V_{1} + V_{2})}{V_{1}}$ , $0$ , $+ v e$

B

$0$ , $R \frac{ln (V_{1} + V_{2})}{V_{1}}$ , $+ v e$

C

$R \frac{ln (V_{1} + V_{2})}{V_{2}}$ , $0$ , $+ v e$

D

$R \frac{ln (V_{2} + V_{1})}{V_{2}}$ , $0$ , $- v e$

Text Solution

Verified by Experts

The correct Answer is:A

|

Updated on:21/07/2023

Class 12 CHEMISTRY CHEMICAL THERMODYNAMICS AND CHEMICAL ENERGETICS

Topper's Solved these Questions

Similar Questions

DINESH PUBLICATION-CHEMICAL THERMODYNAMICS AND CHEMICAL ENERGETICS -Exercise

Home
Ask Doubt
Profile