Entropy has great importance in thermodynamics. It is a state function and it is a measure of the degree of disorder or randomness of the system. More is the disorder of the system, greater will be the entropy and vice versa. It is normally expressed in terms of change of entropy.
(i) For a reaction entropy change is given by ΔS=∑S(product)−∑S(reactant)
(ii)ΔS=QrevT=WrevT=nRTln(V2/V1)T
=nRTln(V2)V1=nRln(P1)P2
(iii)ΔS=ΔH−TΔS
(iv) Entropy change in reversible and irreversible process : Consider a Carnot cycle as shown in figure below in which ab and cd are isothermal.
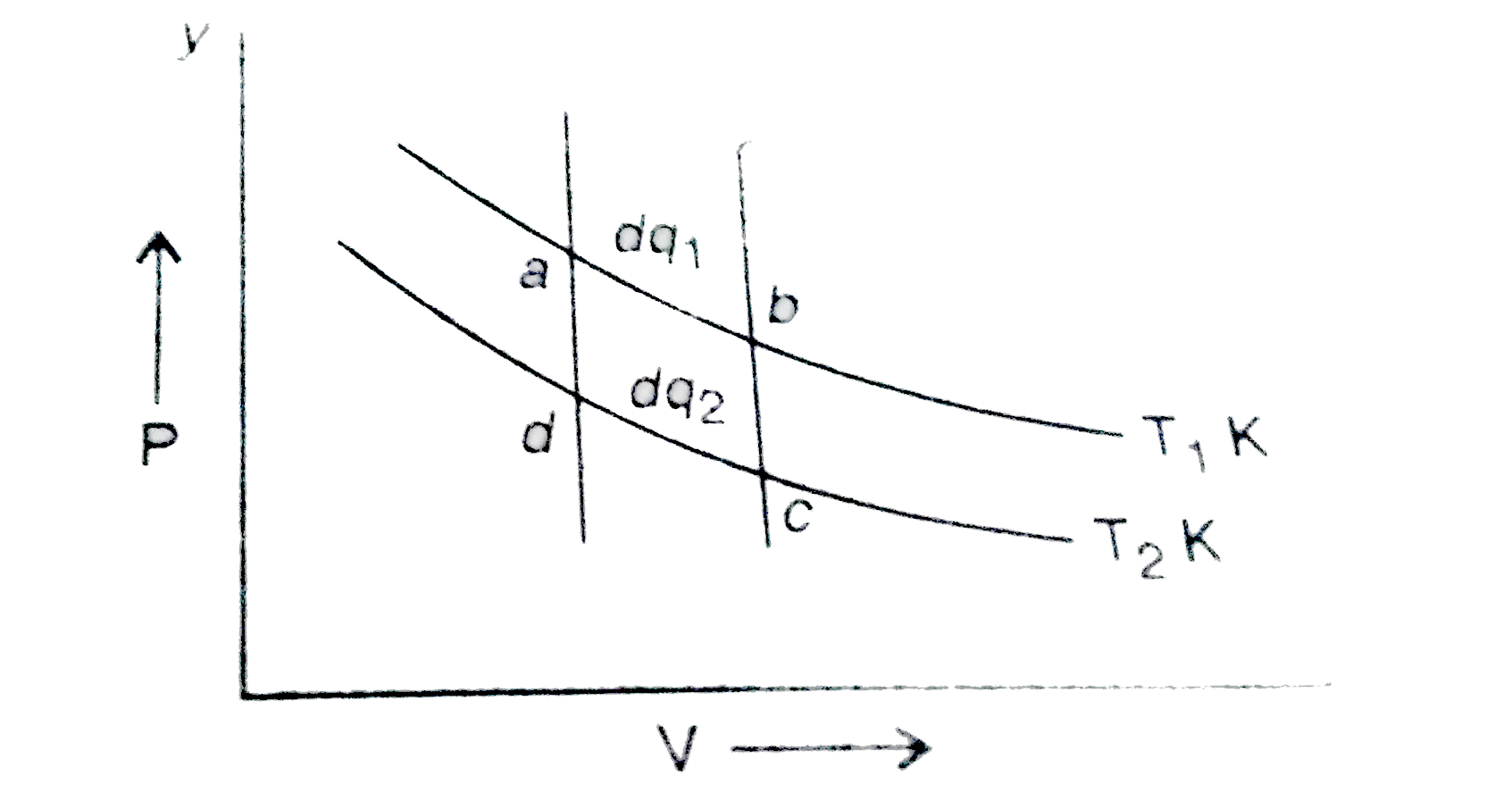
Irrespective of the path of the system in its reversible change, dq/T is same
For entire Carnot cycle
dq1T1−dq2T2=0
∴ΔSuniverse=De<sSsystem+ΔSsurrounding
ΔSSurrounding=q1T1+q2T2 (q term includes their own sign)
bc and da are adiabatics. Let dq1 be the heat supplied to the working system at T1K and dq2 be heat rejected by it to the sink at T2K. All these steps are reversible. In a Carnot cycle.
dq1−dq2dq1=T1−T2T1 or dq1T1=dq2T2
Let us now confine our attention only to the change of the system from point 'a' to point 'c' and attempt to find out the ratio of heat change to the temperature at which thermal changes occur by proceeding from a to c either along abc or adc.
Along the path abc, Heat changeTemp.=dq1T1
Along the path adc, Heat changeTemp=dq2T2
In case of spontaneous and irreversible expansion to volume V1+V2, W=0 and so will be ΔU
In the reversible expansion of the gas at TK from volume V1 to V1+V2, heat absorbed ΔU+RTln(V1+V2)V1
(v) Suppose n moles of an ideal gas are enclosed in a vessel A of volume V1 which is connected through a stop cock to a completely evacuated vessel B of volume V2. The system is insulated and has temperature TK.
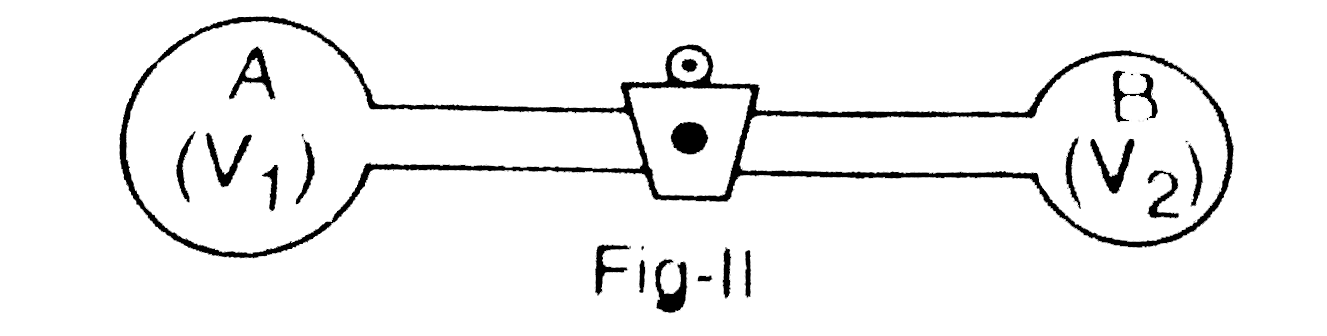
If the stop cock is opened, the gas will attain the volume V1+V2.
In irreversible cyclic process, which of the following is correct ?
ΔSuniverse>0, ΔSsystem=0, ΔSsurround∈gs>0
ΔSuniverse>0, ΔSsystem>0, ΔSsurround∈gs=0
ΔSuniverse>0, ΔSsystem>0, ΔSsurround∈gs=0
ΔSuniverse=0, ΔSsystem=0, ΔSsurround∈gs=0
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
The following initial rate data were obtained at 300K for the reactions:
2A+B→C+D

Deducethe rate law.
View SolutionA copolymer of CH2=CHCl and CH2=CH(OCOCH3) is called
View SolutionThe thermodynamic property that measures the extent of molecular disorder is called entropy. Entropy change of phase transformation can be calculated using Trouton's formula (ΔS=ΔH/T). In the reversible adiabatic process, however, ΔS will be zero. the rise in temperature in isobaric and isochoric conditions is found to increase the randomness or entropy of the system.
ΔS=2.303Clog(T1/T2)
If water in an insulated vessel at −10∘C suddenly freezes, the entropy change of the system will be
View SolutionWork done by the system in isothermal reversible process is wrev.=−2.303nRTlogV2V1. Also in case of adiabatic reversible process work done by the system is given by: wrev.=nRγ−1[T2−T1]. During expansion disorder increases and the increase in disorder is expressed in terms of change in entropy ΔS=qrev.T. The entropy changes also occurs during transformation of one state to other end expressed as ΔS=ΔHT. Both entropy and enthalpy changes obtained for a process were taken as a measure of spontaniety of process but finally it was recommended that decrease in free energy is responsible for spontaniety and ΔG=ΔH−TΔS.
Which statements are correct? (1) The expansion work for a gas into a vacuum is equal to zero. (2) 1 mole of a gas occupying 3 litre volume on expanding to 15 litre at constant pressure of 1atm does expansion work 1.215kJ. (3) The maximum work done during expansion of 16gO2 at 300K from 5dm3 to 25dm3 is 2.01kJ. (4) The ΔS for S→L is almost negligible in comparision to ΔS for L→G. (5) ΔS=2.303nRlogV2V1. (at constant T)
View SolutionWork done by the system in isothermal reversible process is wrev.=−2.303nRTlogV2V1. Also in case of adiabatic reversible process work done by the system is given by: wrev.=nRγ−1[T2−T1]. During expansion disorder increases and the increase in disorder is expressed in terms of change in entropy ΔS=qrev.T. The entropy changes also occurs during transformation of one state to other end expressed as ΔS=ΔHT. Both entropy and enthalpy changes obtained for a process were taken as a measure of spontaniety of process but finally it was recommended that decrease in free energy is responsible for spontaniety and ΔG=ΔH−TΔS.
The heat of vaporisation and heat of fusion of H2O are 540cal/g and 80cal/g. This ratio of ΔSvap.ΔSfusion for water is:
View SolutionWork done by the system in isothermal reversible process is w_(rev.)= -2.303 nRT "log"(V_(2))/(V_(1)) . Also in case of adiabatic reversible process work done by the system is given by: w_(rev.) = (nR)/(gamma -1) [T_2 - T_1] . During expansion disorder increases and the increase in disorder is expressed in terms of change in entropy DeltaS = q_(rev.)/T . The entropy changes also occurs during transformation of one state to other end expressed as DeltaS = DeltaH/T . Both entropy and enthalpy changes obtained for a process were taken as a measure of spontaniety of process but finally it was recommended that decrease in free energy is responsible for spontaniety and DeltaG=DeltaH - T DeltaS . Ag_2O_((s)) to 2Ag_((s)) + 1/2 O_(2(g)) attains equilibrium at temperature… K is : (The DeltaH and DeltaS for the reaction are 30.5kJ mol^(-1) and 66J mol^(-1) K^(-1) )
View SolutionWork done by the system in isothermal reversible process is w_(rev.)= -2.303 nRT "log"(V_(2))/(V_(1)) . Also in case of adiabatic reversible process work done by the system is given by: w_(rev.) = (nR)/(gamma -1) [T_2 - T_1] . During expansion disorder increases and the increase in disorder is expressed in terms of change in entropy DeltaS = q_(rev.)/T . The entropy changes also occurs during transformation of one state to other end expressed as DeltaS = DeltaH/T . Both entropy and enthalpy changes obtained for a process were taken as a measure of spontaniety of process but finally it was recommended that decrease in free energy is responsible for spontaniety and DeltaG=DeltaH - T DeltaS . A chemical change will definitely be spontaneous if:
View SolutionEntropy has great importance in thermodynamics. It is a state function and it is a measure of the degree of disorder or randomness of the system. More is the disorder of the system, greater will be the entropy and vice versa. It is normally expressed in terms of change of entropy. (i) For a reaction entropy change is given by DeltaS=sumS("product")-sumS("reactant") (ii) DeltaS=(Q_(rev))/(T)=(W_(rev))/(T)=(nRT ln (V_(2)//V_(1)))/(T) =nRT ln (V_(2))/(V_(1))=nR ln (P_(1))/(P_(2)) (iii) DeltaS=DeltaH-TDeltaS (iv) Entropy change in reversible and irreversible process : Consider a Carnot cycle as shown in figure below in which ab and cd are isothermal. Irrespective of the path of the system in its reversible change, dq//T is same For entire Carnot cycle (dq_(1))/(T_(1))-(dq_(2))/(T_(2))=0 :. DeltaS_("universe")=DeltsS_("system")+DeltaS_("surrounding") DeltaS_("Surrounding")=(q_(1))/(T_(1))+(q_(2))/(T_(2)) ( q term includes their own sign) bc and da are adiabatics. Let dq_(1) be the heat supplied to the working system at T_(1) K and dq_(2) be heat rejected by it to the sink at T_(2) K . All these steps are reversible. In a Carnot cycle. (dq_(1)-dq_(2))/(dq_(1))=(T_(1)-T_(2))/(T_(1)) or (dq_(1))/(T_(1))=(dq_(2))/(T_(2)) Let us now confine our attention only to the change of the system from point 'a' to point 'c' and attempt to find out the ratio of heat change to the temperature at which thermal changes occur by proceeding from a to c either along abc or adc . Along the path abc , ("Heat change")/("Temp.")=(dq_(1))/(T_(1)) Along the path adc , ("Heat change")/("Temp")=(dq_(2))/(T_(2)) In case of spontaneous and irreversible expansion to volume V_(1)+V_(2) , W=0 and so will be DeltaU In the reversible expansion of the gas at T K from volume V_(1) to V_(1)+V_(2) , heat absorbed DeltaU+RT ln (V_(1)+V_(2))/(V_(1)) (v) Suppose n moles of an ideal gas are enclosed in a vessel A of volume V_(1) which is connected through a stop cock to a completely evacuated vessel B of volume V_(2) . The system is insulated and has temperature T K . If the stop cock is opened, the gas will attain the volume V_(1)+V_(2) . Which of the following statement is correct about entropy ?
View SolutionEntropy has great importance in thermodynamics. It is a state function and it is a measure of the degree of disorder or randomness of the system. More is the disorder of the system, greater will be the entropy and vice versa. It is normally expressed in terms of change of entropy. (i) For a reaction entropy change is given by DeltaS=sumS("product")-sumS("reactant") (ii) DeltaS=(Q_(rev))/(T)=(W_(rev))/(T)=(nRT ln (V_(2)//V_(1)))/(T) =nRT ln (V_(2))/(V_(1))=nR ln (P_(1))/(P_(2)) (iii) DeltaS=DeltaH-TDeltaS (iv) Entropy change in reversible and irreversible process : Consider a Carnot cycle as shown in figure below in which ab and cd are isothermal. Irrespective of the path of the system in its reversible change, dq//T is same For entire Carnot cycle (dq_(1))/(T_(1))-(dq_(2))/(T_(2))=0 :. DeltaS_("universe")=DeltsS_("system")+DeltaS_("surrounding") DeltaS_("Surrounding")=(q_(1))/(T_(1))+(q_(2))/(T_(2)) ( q term includes their own sign) bc and da are adiabatics. Let dq_(1) be the heat supplied to the working system at T_(1) K and dq_(2) be heat rejected by it to the sink at T_(2) K . All these steps are reversible. In a Carnot cycle. (dq_(1)-dq_(2))/(dq_(1))=(T_(1)-T_(2))/(T_(1)) or (dq_(1))/(T_(1))=(dq_(2))/(T_(2)) Let us now confine our attention only to the change of the system from point 'a' to point 'c' and attempt to find out the ratio of heat change to the temperature at which thermal changes occur by proceeding from a to c either along abc or adc . Along the path abc , ("Heat change")/("Temp.")=(dq_(1))/(T_(1)) Along the path adc , ("Heat change")/("Temp")=(dq_(2))/(T_(2)) In case of spontaneous and irreversible expansion to volume V_(1)+V_(2) , W=0 and so will be DeltaU In the reversible expansion of the gas at T K from volume V_(1) to V_(1)+V_(2) , heat absorbed DeltaU+RT ln (V_(1)+V_(2))/(V_(1)) (v) Suppose n moles of an ideal gas are enclosed in a vessel A of volume V_(1) which is connected through a stop cock to a completely evacuated vessel B of volume V_(2) . The system is insulated and has temperature T K . If the stop cock is opened, the gas will attain the volume V_(1)+V_(2) . Ethanol boils at 78.4^(@)C and standard enthalpy of vaporisation of ethanol is 42.4 kJ//mol . Calculate the enthropy of vaporisation of ethanol
View SolutionEntropy has great importance in thermodynamics. It is a state function and it is a measure of the degree of disorder or randomness of the system. More is the disorder of the system, greater will be the entropy and vice versa. It is normally expressed in terms of change of entropy.
(i) For a reaction entropy change is given by ΔS=∑S(product)−∑S(reactant)
(ii)ΔS=QrevT=WrevT=nRTln(V2/V1)T
=nRTln(V2)V1=nRln(P1)P2
(iii)ΔS=ΔH−TΔS
(iv) Entropy change in reversible and irreversible process : Consider a Carnot cycle as shown in figure below in which ab and cd are isothermal.
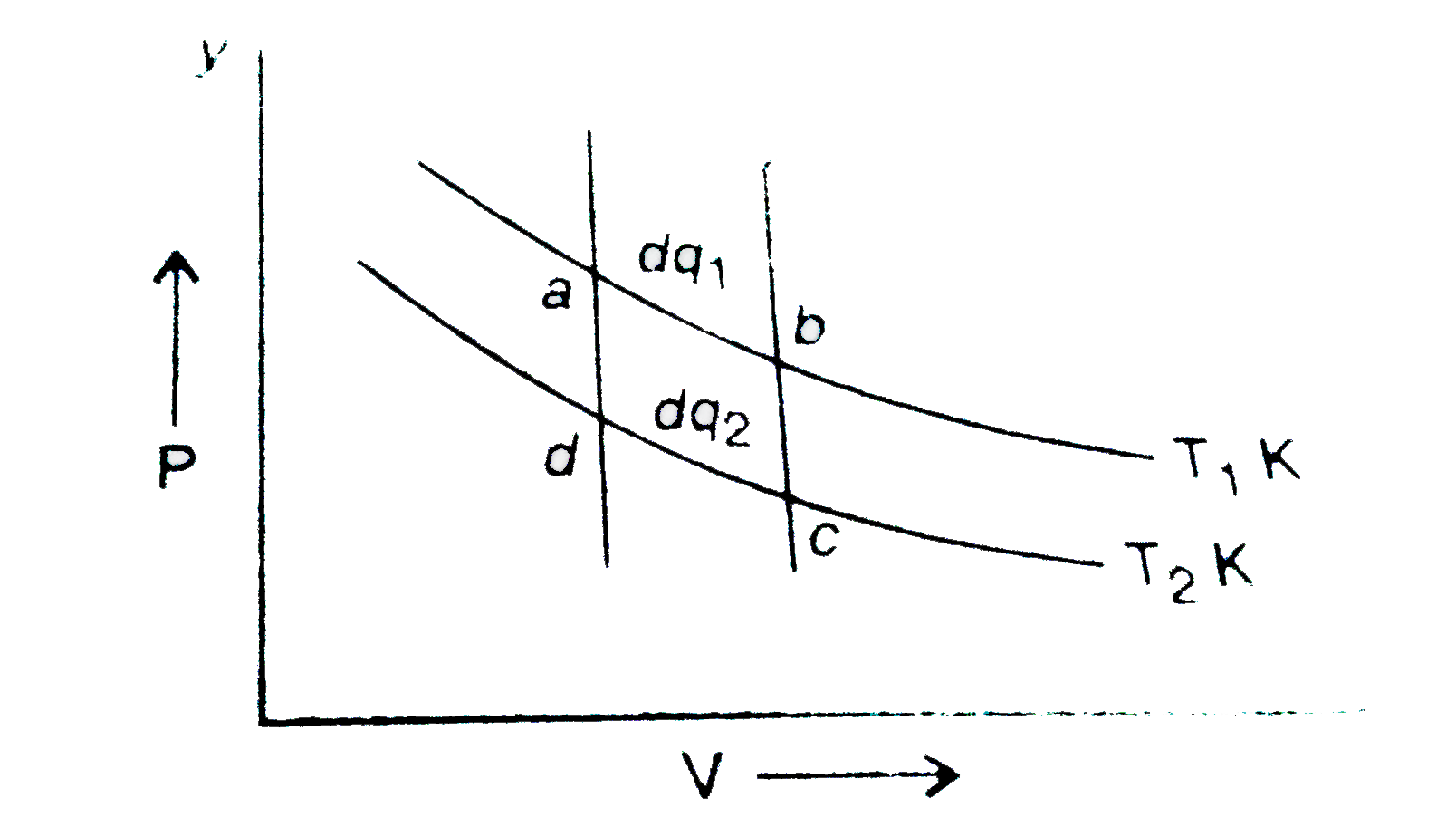
Irrespective of the path of the system in its reversible change, dq/T is same
For entire Carnot cycle
dq1T1−dq2T2=0
∴ΔSuniverse=De<sSsystem+ΔSsurrounding
ΔSSurrounding=q1T1+q2T2 (q term includes their own sign)
bc and da are adiabatics. Let dq1 be the heat supplied to the working system at T1K and dq2 be heat rejected by it to the sink at T2K. All these steps are reversible. In a Carnot cycle.
dq1−dq2dq1=T1−T2T1 or dq1T1=dq2T2
Let us now confine our attention only to the change of the system from point 'a' to point 'c' and attempt to find out the ratio of heat change to the temperature at which thermal changes occur by proceeding from a to c either along abc or adc.
Along the path abc, Heat changeTemp.=dq1T1
Along the path adc, Heat changeTemp=dq2T2
In case of spontaneous and irreversible expansion to volume V1+V2, W=0 and so will be ΔU
In the reversible expansion of the gas at TK from volume V1 to V1+V2, heat absorbed ΔU+RTln(V1+V2)V1
(v) Suppose n moles of an ideal gas are enclosed in a vessel A of volume V1 which is connected through a stop cock to a completely evacuated vessel B of volume V2. The system is insulated and has temperature TK.
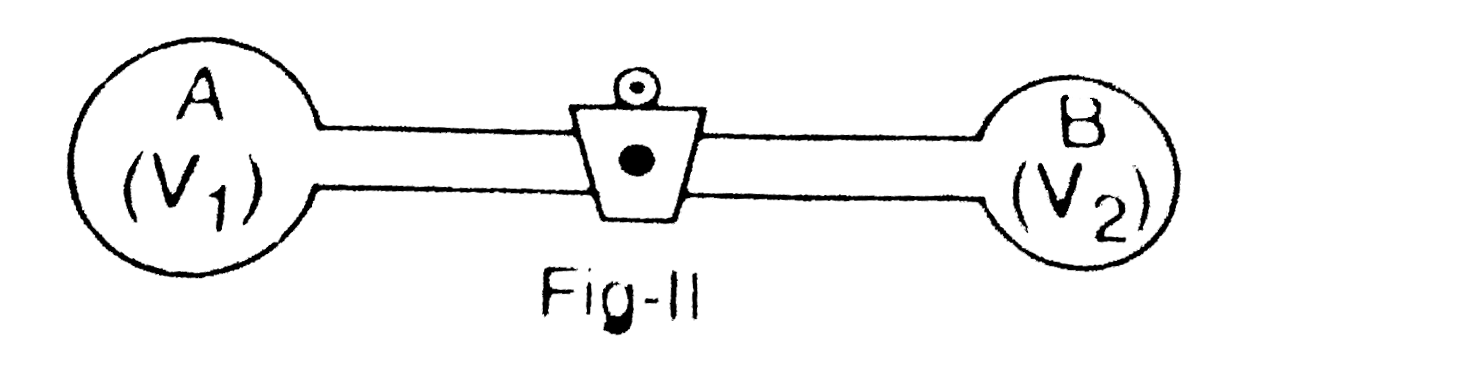
If the stop cock is opened, the gas will attain the volume V1+V2.
In the figure-I, what will be the value of dqT along the line bc ?
View SolutionEntropy has great importance in thermodynamics. It is a state function and it is a measure of the degree of disorder or randomness of the system. More is the disorder of the system, greater will be the entropy and vice versa. It is normally expressed in terms of change of entropy. (i) For a reaction entropy change is given by DeltaS=sumS("product")-sumS("reactant") (ii) DeltaS=(Q_(rev))/(T)=(W_(rev))/(T)=(nRT ln (V_(2)//V_(1)))/(T) =nRT ln (V_(2))/(V_(1))=nR ln (P_(1))/(P_(2)) (iii) DeltaS=DeltaH-TDeltaS (iv) Entropy change in reversible and irreversible process : Consider a Carnot cycle as shown in figure below in which ab and cd are isothermal. Irrespective of the path of the system in its reversible change, dq//T is same For entire Carnot cycle (dq_(1))/(T_(1))-(dq_(2))/(T_(2))=0 :. DeltaS_("universe")=DeltsS_("system")+DeltaS_("surrounding") DeltaS_("Surrounding")=(q_(1))/(T_(1))+(q_(2))/(T_(2)) ( q term includes their own sign) bc and da are adiabatics. Let dq_(1) be the heat supplied to the working system at T_(1) K and dq_(2) be heat rejected by it to the sink at T_(2) K . All these steps are reversible. In a Carnot cycle. (dq_(1)-dq_(2))/(dq_(1))=(T_(1)-T_(2))/(T_(1)) or (dq_(1))/(T_(1))=(dq_(2))/(T_(2)) Let us now confine our attention only to the change of the system from point 'a' to point 'c' and attempt to find out the ratio of heat change to the temperature at which thermal changes occur by proceeding from a to c either along abc or adc . Along the path abc , ("Heat change")/("Temp.")=(dq_(1))/(T_(1)) Along the path adc , ("Heat change")/("Temp")=(dq_(2))/(T_(2)) In case of spontaneous and irreversible expansion to volume V_(1)+V_(2) , W=0 and so will be DeltaU In the reversible expansion of the gas at T K from volume V_(1) to V_(1)+V_(2) , heat absorbed DeltaU+RT ln (V_(1)+V_(2))/(V_(1)) (v) Suppose n moles of an ideal gas are enclosed in a vessel A of volume V_(1) which is connected through a stop cock to a completely evacuated vessel B of volume V_(2) . The system is insulated and has temperature T K . If the stop cock is opened, the gas will attain the volume V_(1)+V_(2) . In figure I , which is a reversible cyclic process, what will be the value of DeltaU , DeltaH , oint(dq)/(T) respectively ?
View SolutionEntropy has great importance in thermodynamics. It is a state function and it is a measure of the degree of disorder or randomness of the system. More is the disorder of the system, greater will be the entropy and vice versa. It is normally expressed in terms of change of entropy. (i) For a reaction entropy change is given by DeltaS=sumS("product")-sumS("reactant") (ii) DeltaS=(Q_(rev))/(T)=(W_(rev))/(T)=(nRT ln (V_(2)//V_(1)))/(T) =nRT ln (V_(2))/(V_(1))=nR ln (P_(1))/(P_(2)) (iii) DeltaS=DeltaH-TDeltaS (iv) Entropy change in reversible and irreversible process : Consider a Carnot cycle as shown in figure below in which ab and cd are isothermal. Irrespective of the path of the system in its reversible change, dq//T is same For entire Carnot cycle (dq_(1))/(T_(1))-(dq_(2))/(T_(2))=0 :. DeltaS_("universe")=DeltsS_("system")+DeltaS_("surrounding") DeltaS_("Surrounding")=(q_(1))/(T_(1))+(q_(2))/(T_(2)) ( q term includes their own sign) bc and da are adiabatics. Let dq_(1) be the heat supplied to the working system at T_(1) K and dq_(2) be heat rejected by it to the sink at T_(2) K . All these steps are reversible. In a Carnot cycle. (dq_(1)-dq_(2))/(dq_(1))=(T_(1)-T_(2))/(T_(1)) or (dq_(1))/(T_(1))=(dq_(2))/(T_(2)) Let us now confine our attention only to the change of the system from point 'a' to point 'c' and attempt to find out the ratio of heat change to the temperature at which thermal changes occur by proceeding from a to c either along abc or adc . Along the path abc , ("Heat change")/("Temp.")=(dq_(1))/(T_(1)) Along the path adc , ("Heat change")/("Temp")=(dq_(2))/(T_(2)) In case of spontaneous and irreversible expansion to volume V_(1)+V_(2) , W=0 and so will be DeltaU In the reversible expansion of the gas at T K from volume V_(1) to V_(1)+V_(2) , heat absorbed DeltaU+RT ln (V_(1)+V_(2))/(V_(1)) (v) Suppose n moles of an ideal gas are enclosed in a vessel A of volume V_(1) which is connected through a stop cock to a completely evacuated vessel B of volume V_(2) . The system is insulated and has temperature T K . If the stop cock is opened, the gas will attain the volume V_(1)+V_(2) . In a reversible isothermal expansion of the gas at T K as shown in figure II , the DeltaS_("system") , DeltaS_("surroundings") and DeltaS_("universe") will be respectively ?
View SolutionEntropy ( S ) is a thermodynamic variable like pressure P , volume V and temperature T . Entropy of a thermodynamic system is a measure of disorder of molecular motion. Greater is disorder , greater is entropy. Change in entropy of a thermodynamic system is the ratio of heat supplied to absolute temperature.In an adiabatic reversible process, entropy remains constant while in any irreversible process entropy increases. In nature the processes are irreversible , therefore entropy of universe is continuoulsy increasing. The unit of entropy in S-I system is -
View SolutionEntropy ( S ) is a thermodynamic variable like pressure P , volume V and temperature T . Entropy of a thermodynamic system is a measure of disorder of molecular motion. Greater is disorder , greater is entropy. Change in entropy of a thermodynamic system is the ratio of heat supplied to absolute temperature.In an adiabatic reversible process, entropy remains constant while in any irreversible process entropy increases. In nature the processes are irreversible , therefore entropy of universe is continuoulsy increasing. When milk is heated , its entropy :
View SolutionExplain change in entropy of a system during a reversible process Delta S = (q_(rev))/(T)
View Solution
