The rate law for decomposition N2O5 is rate =k[N2O5]
What is the significance of k in the equation?
k corresponds the rate constant.
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - Effect of temperature and catalyst on rate of reaction.
15 Videos
- CHEMICAL KINETICSBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - Select the correct answer.
100 Videos
- CHEMICAL KINETICSBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - Assertion Reason type questions
5 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Unit Test - 1
20 Videos
- CHEMICAL THERMODYNAMICS AND CHEMICAL ENERGETICS BOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL THERMODYNAMICS AND CHEMICAL ENERGETICS EXERCISE - Exercise
507 Videos
Similar Questions
Knowledge Check
The rate law of the reaction 2N2O5→4NO2+O2 is
ARate = K[NO2]4[O2]BRate =K[N2O5]2CRate =K[N2O5]0DRate =K[N2O5]The rate equation for the decomposition of N2O5 in CCl4 is rate =K[N2O5], where K=6.3×10−4s−1 at 320K. What would be the initial rate of decomposition of N2O5 in a 0.10M solution of N2O5 ?
A(a) 6.3×10−6mollitre−1s−1B(b) 0.63×10−6mollitre−1s−1C(c ) 6.3×10−5mollitre−1s−1D(d) 0.63×10−4mollitre−1s−1What is the activation energy for the decomposition of N2O5 as
N2O5⇔2NO2+12O2
If the values of the rate constants are 3.45×10−5 and 6.9×10−3 at 27∘C and 67∘C respectivelyA102×102kJB488.5kJC112kJD14.7kJ
The experiment data for decomposition of N2O5[2N2O5→4NO2+O2] in gas phase at 318 K are given below:

a) Plot [N2O5] against t
b) Find the half life period for the reaction.
c) Draw a graph between log [N2O5] and t
d) What is rate law?
e) Calculate the rate constant
f) Calculate the half life period from k and compare it with (b)
View SolutionThe experimental data for decomposition of N2O5
[2N2O5→4NO2+O2]
in gas phase at 318K are given below:
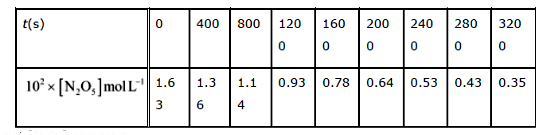
(i) Plot [N2O5] against t.
(ii) Find the half-life period for the reaction.
(iii) Draw a graph between log[N2O5] and t.
(iv) What is the rate law ?
(v) Calculate the rate constant.
(vi) Calculate the half-life period from k and compare it with (ii).
View SolutionThe experimental data for the decomposition of N2O5,[2N2O5→4NO2+O2] in gas phase at 318 K are given below:

(i) Plot [N2O5] against t.
(ii) Find the half-life period for the reaction.
(iii) Draw a graph between log[N2O5] and t.
(iv) What is the rate law?
(v) Calculate the rate constant.
(vi) Calculate the half-life period from k and compare it with (ii).
View SolutionUsing the concentration time equation for a first order reaction : The decomposition of N2O5 to NO2 and O2 is first order, with a rate constant of 4.80×10−4/sa45∘C
N2O5(g)→2NO2(g)+12O2(g)
(a) If the initial concentration of N2O5is1.65×10−2mol/L, what is its concentration after 825 s ?
(b) How long would it take for the concentration of N2O5 to decrease to 100×10−2molL−1 from its initiqal value, given in (a) ?
Strategy : Since this reaction has a first order rate law, d[N2O5]/dt=k[N2O5] , we can use the corresaponding concentration time equation for a first order reaction :
k=2.303tlog([N2O5]0)[N2O5]t
In each part, we substitute the know quantities into this equation and solve for the unkbnown.
View SolutionThe reaction :
N2O5(in(C)Cl4solution)→2NO2(same solution)+1/2O2(g) is of first order in N2O5 with rate constant = 6.2×10−4s−1. What is the value of the rate of reaction when [N2O5] with rate constant = 6.2×10−4s−1. What is the rate of reaction when N2O5=12.5molL−1?
View Solution
