एक बड़े, खुले मुँह के, नगण्य द्रव्यमान व एकसमान परिच्छेद-क्षेत्रफल A वाले बर्तन की तली के समीप बर्तन की दीवार में एक सूक्ष्म छिद्र है जिसका परिच्छेद-क्षेत्रफल A/100 है। यह बर्तन चिकने क्षैतिज फर्श पर रखा है तथा इसमें द्रव्यमान m0 व घनत्व ρ का द्रव भरा है। यह मान कर कि द्रव का समय t=0 पर, छिद्र में से क्षैतिज प्रवाह प्रारम्भ होता है, गणना कीजिए
(a) बर्तन का त्वरण तथा
(b) इसका वेग जबकि इसमें से 75% द्रव निकल चुका है।
(g=10 मी/से2)
The correct Answer is:(a) g50 (b) √gm02Aρ
जल का द्रव्यमान = आयतन × घनत्व
∴m0=(AH)ρ
⇒H=m0Aρ ...(i)
प्रवाह वेग, v=√2gH=√2g.m0Aρ या v=√2m0gAρ
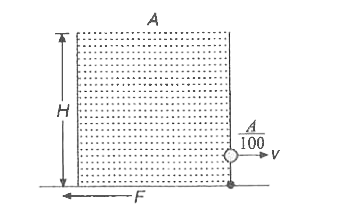
द्रव के छिद्र से बाहर निकलने के कारण बर्तन पर कार्य करने वाला उत्प्लावन बल
F = (द्रव का घनत्व) (छिद्र का क्षेत्रफल) (प्रवाह वेग)2
या F=ρav2=ρ(A/100)v2=ρ(A100)(2m0gAρ)
या F=m0g50
इसलिए बर्तन का त्वरण
a=Fm0=g50
(b) 75% द्रव बाहर निकलने पर

h=H4=m04Aρ
प्रवाह वेग,
v=√2gh=√2g(m04Aρ)=√m0g2Aρ
Topper's Solved these Questions
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-I)
3 Videos
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-II)
3 Videos
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - एकल पूर्णांक उत्तर प्रकार
6 Videos
- धारा वैघुतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - धारा वैघुतिकी EXERCISE - क्षृंखलाबद्ध-बोधन प्रकार (अनुछेद I )
2 Videos
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - श्रृंखलाबद्ध - बोधन प्रकार
5 Videos
Similar Questions
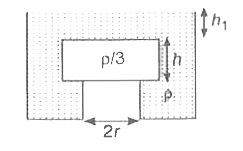
एक लकड़ी का बेलन जिसका व्यास 4r, ऊंचाई h तथा घनत्व ρ/3 है। एक 2r व्यास की टंकी वाले छिद्र पर रखा है। टंकी ρ घनत्व वाले द्रव से भरी है।
द्रव का स्तर धीरे-धीरे नीचे गिरने लगता है जब बेलन के ऊपर द्रव स्तर की ऊँचाई h1 है, तब ब्लॉक ऊपर गति करना प्रारम्भ करता है। h1 के किस मान पर ब्लॉक उठेगा?
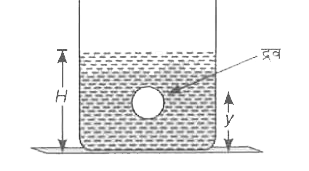
View Solutionएकपरमाणुक आदर्श गैस का छोटा बुलबुला (γ=53),ρl घनत्व वाले द्रव से घिरा हुआ है। माना कि यह बुलबुला द्रव से किसी प्रकार का ऊष्मीय आदान-प्रदान नहीं करता। बुलबुले में गैस के n मोल है। बुलबुला जब तली में स्थित है तब गैस का ताप T0 है, द्रव स्तम्भ की ऊँचाई H है तथा वायुमंडलीय दाब p0 है (पृष्ठ तनाव नगण्य है)
जैसे-जैसे बुलबुला ऊपर की ओर गति करता है, उत्प्लावन बल के अतिरिक्त जो बल उस पर कार्य करते है,वह है-
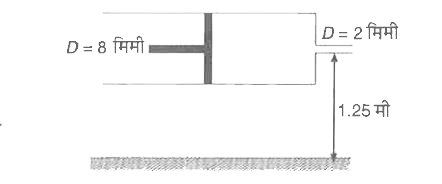
View Solutionपृथ्वी तल से 1.25 मी की ऊँचाई पर क्षैतिज दिशा में स्थित पिचकारी जल से भरी है। निमज्जक का व्यास 8 मिमी तथा तुंड का व्यास 2 मिमी है। निमज्जक को 0.25 मी/से की नियत चाल से दबाया जाता है। पृथ्वी तल पर पानी की धारा की क्षैतिज परास ज्ञात कीजिए (g=10 मी/से2)
View Solutionh ऊँचाई वाले निर्वातित एक बेलनाकार कक्ष के दोनों छोरो पर दो दृढ़ चालक पट्टिकाएं है और उसका वक्रपृष्ठ अचालक है, जैसा की चित्र में दर्शाया गया है। कम भार वाली मुलायम पदार्थ से बनी हुई कई गोलाकार गोलियाँ, जिनकी सतह पर एक चालक पदार्थ की परत चढ़ी है, नीचे वाली पट्टिका पर रखी हुई है। इन गोलियों की त्रिज्या r<<h है। अब एक उच्च वोल्टता का स्त्रोत इस प्रकार से जोड़ा जाता है कि नीचे वाली पट्टिका पर +V0 एवं ऊपर वाली पट्टिका पर −V0 का विभव आ जाता है। चालक परत के कारण गोलियाँ आवेशित होकर पट्टिका के साथ समविभव हो जाती है जिसके कारण वे पट्टिका से प्रतिकर्षित होती है। अंततोगत्वा गोलियाँ ऊपरी पट्टिका से टकराती है, जहाँ पर गोलियों के पदार्थ की मुलायम प्रकृति के कारण प्रत्यवस्थान गुणांक को शून्य लिया जा सकता है। कक्ष में विद्युत क्षेत्र को समानान्तर पट्टिका वाले संधारित्र के माना जा सकता है। गोलियों की एक दूसरे से पारस्परिक क्रिया एवं टकराव को नगण्य माना जा सकता है (गुरुत्वाकर्षण नगण्य है।)

निम्नलिखित में से कौनसा कथन सत्य है?
View Solutionचित्र में XY एक पृष्ठ है जो दो पारदर्शी माध्यमों, माध्यम -1 तथा माध्यम -2 को अलग करता है | रेखाएँ ab तथा cd माध्यम -1 में चल रहीं तथा पृष्ठ XY पर आपतित होने वाली प्रकाश - तरंग के तरंग्रागों को निरूपित करती हैं | रेखाएँ ef तथा gh अपवर्तन के बाद माध्यम -2 में चल रही प्रकाश तरंग के तरंग्रागों को निरूपित करती हैं |
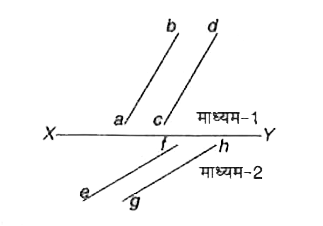
प्रकाश चल रहा ह
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionमाना एक वृत्त है जिसका केन्द्र परवलय y2=2px की नाभि पर है, तथा यह वृत्त परवलय की नियता को स्पर्श करता है, तो वृत्त व परवलय का प्रतिच्छेद बिंदू है
View Solutionचीनी मिट्टी के बर्तन का टूटना एक अनुत्क्रमणीय भौतिक परिवर्तन है।
View SolutionThe internal diameter of a hollow hemispherical vessel is 24 cm. It is made of a steel sheet which is 0.5 cm thick. What is the total surface area (in cm2) of the vessel ?
एक खोखले अर्धगोलीय बर्तन का आतंरिक व्यास 24 सेमी है | यह इस्पात की चादर से बना हुआ है जिसकी मोटाई 0.5 सेमी है | इस बर्तन का कुल पृष्ठ क्षेत्रफल ( वर्ग सेमी में) ज्ञात करें |
View Solutionनिम्नांकित गद्य खण्ड को पढ़कर प्रश्न के उत्तर दीजिए
भारतीय संस्कृति विश्व की प्राचीनतम संस्कृतियों में से एक है। यह एक बड़ी भारी सामाजिक विरासत है, जिसके पीछे लम्बा इतिहास है। रामायण और महाभारत जैसे ग्रन्थ इसी विरासत का एक भाग हैं जिन पर हमें गर्व है। देश की सभ्यता व संस्कृति का इतिहास बहुत पुराना है। भारत में जन्म लेने वाले महापुरुषों ने समय-समय पर इस देश की कीर्ति पताका विश्व में फैलाई है। महर्षि पाणिनि से लेकर वाल्मीकि, वेदव्यास, सूर, तुलसी एवं महर्षि विवेकानन्द, गांधी और गौतम के रूप में यह परम्परा चलती रही।
संस्कृति से किस बात का बोध होता है?
View SolutionIn a U-tube, the radii of the two pillars are respectively r_1 " और " r_2 Huh. When rho (theta = 0^@) घनत्व का एक द्रव इसमें भरा जाता है, तो दो भुजाओं के स्तर में h | का अंतर देखा जाता है। द्रव का पृष्ठ तनाव है:
View Solutionदो गैसों का एक भूरे रंग का मिश्रण धातु कॉपर के साथ 6N नाइट्रिक अम्ल के अपचयन से प्राप्त किया जाता है। शीतलन पर यह मिश्रण एक नीले द्रव में संघनित होता है, जो -30^@C पर जमने पर एक नीला ठोस देता है। नीले द्रव या ठोस के लिए सही विकल्प है:
View Solution1 atm के बाह्य दाब के अंतर्गत गतिशील पिस्टन वाले एक निर्वातित पात्र में, He के 0.1 मोल और एक अज्ञात यौगिक के 1.0 मोल (0°C पर 0.68 atm वाष्प दाब) को रखा जाता है। आदर्श गैस व्यवहार मानते हुए, 0°C पर साम्यावस्था पर गैस का कुल आयतन (L में) लगभग x L के समान है। x के मान की गणना कीजिए।
View Solution1.0 mg के द्रव्यमान वाले एक कण का वेग 3600 km/h है। कण के तरंग दैर्ध्य की गणना कीजिए।
View Solution
