एक बेलनाकार टंकी जिसकी ऊपरी त्रिज्या 0.9 मी तथा निचली त्रिज्या 0.3 मी है, 900किग्रा/मी3 घनत्व वाले द्रव से भरा है। लम्बाई l की एक केशनली टंकी के निचले सिरे से चित्रानुसार जुडी है। केशनली की बाहरी त्रिज्या 0.002 मी तथा आंतरिक त्रिज्या a मी है। जब टंकी के ऊपरी सिरे पर दाब p आरोपित किया जाता है तो द्रव प्रवाह की दर 8×10−6 मी3/से है तथा यदि केशनली को टंकी से अलग कर दिया जाए, तो द्रव 10 मी/से के वेग से बाहर निकलता है। द्रव के श्यानता गुणांक की गणना कीजिए।
(πa2=10−6 मी2, तथा a2l=2×10−6 मी)
The correct Answer is:1720¯¯¯¯¯मी2
नलिका की अनुपस्थिति में
p+p0+12ρv21+ρgh=12ρv22+p0
∴p+ρgH=12ρ(v22−v21)
पुनः A1v1=A2v2 या v1=A2v2A1
∴p+ρgH=12×ρ[v22−(A2A1v2)2]
=12×ρv22⎡⎣1−(π(0.3)2π(0.9)2)2⎤⎦
=12×ρ×(10)2[1−181]=4×103ρ81
या p+ρgH=49×105 न्यूटन/मी2
यही अतिरिक्त दाब Δp है।
प्वायजली के समीकरण से केशनली में द्रव के प्रवाह की दर
Q=π(Δp)a48ηl
∴8×10−6=(πa2)(Δp)8η(a2l)
⇒η=(πa2)(Δp)(a2l)8×8×10−6
=(10−6)(49×105)(2×10−6)8×8×10−6
=1720 न्यूटन-से/मी2
Topper's Solved these Questions
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-I)
3 Videos
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-II)
3 Videos
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - एकल पूर्णांक उत्तर प्रकार
6 Videos
- धारा वैघुतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - धारा वैघुतिकी EXERCISE - क्षृंखलाबद्ध-बोधन प्रकार (अनुछेद I )
2 Videos
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - श्रृंखलाबद्ध - बोधन प्रकार
5 Videos
Similar Questions
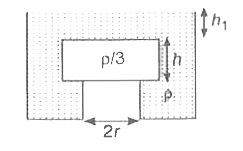
एक लकड़ी का बेलन जिसका व्यास 4r, ऊंचाई h तथा घनत्व ρ/3 है। एक 2r व्यास की टंकी वाले छिद्र पर रखा है। टंकी ρ घनत्व वाले द्रव से भरी है।
द्रव का स्तर धीरे-धीरे नीचे गिरने लगता है जब बेलन के ऊपर द्रव स्तर की ऊँचाई h1 है, तब ब्लॉक ऊपर गति करना प्रारम्भ करता है। h1 के किस मान पर ब्लॉक उठेगा?
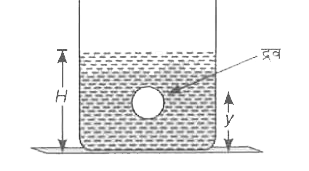
View Solutionएकपरमाणुक आदर्श गैस का छोटा बुलबुला (γ=53),ρl घनत्व वाले द्रव से घिरा हुआ है। माना कि यह बुलबुला द्रव से किसी प्रकार का ऊष्मीय आदान-प्रदान नहीं करता। बुलबुले में गैस के n मोल है। बुलबुला जब तली में स्थित है तब गैस का ताप T0 है, द्रव स्तम्भ की ऊँचाई H है तथा वायुमंडलीय दाब p0 है (पृष्ठ तनाव नगण्य है)
जैसे-जैसे बुलबुला ऊपर की ओर गति करता है, उत्प्लावन बल के अतिरिक्त जो बल उस पर कार्य करते है,वह है-
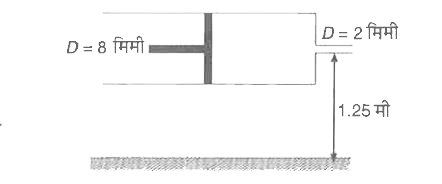
View Solutionपृथ्वी तल से 1.25 मी की ऊँचाई पर क्षैतिज दिशा में स्थित पिचकारी जल से भरी है। निमज्जक का व्यास 8 मिमी तथा तुंड का व्यास 2 मिमी है। निमज्जक को 0.25 मी/से की नियत चाल से दबाया जाता है। पृथ्वी तल पर पानी की धारा की क्षैतिज परास ज्ञात कीजिए (g=10 मी/से2)
View Solutionh ऊँचाई वाले निर्वातित एक बेलनाकार कक्ष के दोनों छोरो पर दो दृढ़ चालक पट्टिकाएं है और उसका वक्रपृष्ठ अचालक है, जैसा की चित्र में दर्शाया गया है। कम भार वाली मुलायम पदार्थ से बनी हुई कई गोलाकार गोलियाँ, जिनकी सतह पर एक चालक पदार्थ की परत चढ़ी है, नीचे वाली पट्टिका पर रखी हुई है। इन गोलियों की त्रिज्या r<<h है। अब एक उच्च वोल्टता का स्त्रोत इस प्रकार से जोड़ा जाता है कि नीचे वाली पट्टिका पर +V0 एवं ऊपर वाली पट्टिका पर −V0 का विभव आ जाता है। चालक परत के कारण गोलियाँ आवेशित होकर पट्टिका के साथ समविभव हो जाती है जिसके कारण वे पट्टिका से प्रतिकर्षित होती है। अंततोगत्वा गोलियाँ ऊपरी पट्टिका से टकराती है, जहाँ पर गोलियों के पदार्थ की मुलायम प्रकृति के कारण प्रत्यवस्थान गुणांक को शून्य लिया जा सकता है। कक्ष में विद्युत क्षेत्र को समानान्तर पट्टिका वाले संधारित्र के माना जा सकता है। गोलियों की एक दूसरे से पारस्परिक क्रिया एवं टकराव को नगण्य माना जा सकता है (गुरुत्वाकर्षण नगण्य है।)

निम्नलिखित में से कौनसा कथन सत्य है?
View Solutionचित्र में XY एक पृष्ठ है जो दो पारदर्शी माध्यमों, माध्यम -1 तथा माध्यम -2 को अलग करता है | रेखाएँ ab तथा cd माध्यम -1 में चल रहीं तथा पृष्ठ XY पर आपतित होने वाली प्रकाश - तरंग के तरंग्रागों को निरूपित करती हैं | रेखाएँ ef तथा gh अपवर्तन के बाद माध्यम -2 में चल रही प्रकाश तरंग के तरंग्रागों को निरूपित करती हैं |
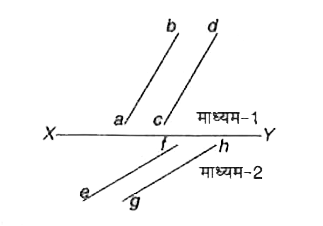
प्रकाश चल रहा ह
View Solution22 मी. × 20 मी. आयताकार छत से एक बेलनाकार पात्र जिसका व्यास 2 मी. तथा ऊंचाई 3.5 मी. है में पानी गिरता है। यदि पात्र पूरा भरा हुआ हो तब होई हुई वर्षा (सेमी. में) में ज्ञात करें?
View Solutionपृथ्वी की त्रिज्या 6.4×106 मी है। पृथ्वी-तल से 800 किमी की ऊँचाई पर गुरुत्वीय विभव तथा गुरुत्वीय क्षेत्र की तीव्रता ज्ञात कीजिए। (g=10 मी/से.2)
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionकिसी बेलन का अर्धव्यास 2 मी/से की दर से बढ़ता है और ऊँचाई 3 मी/से की दर से घटती है। जब उसकी ऊँचाई 5 मी और अर्धव्यास 3 मी हो, तो बेलन के आयतन के परिवर्तन की दर होगी
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionयदि शंकु की त्रिज्या 5 से. मी. हो, तो उसका व्यास होगा
View Solutionयदि बेलन का व्यास 20 से. मी. है, तो उसकी त्रिज्या होगी
View Solutionएक धातु के बेलन को, जिसका व्यास 8 से.मी. और ऊँचाई 90 से. मी. है, गलाकर 12 से. मी. व्यास वाले कितने गोले बनाए जा सकते हैं ?
View Solution
