एक आर्दश गैस उत्क्रमणीय स्थैतिक - कल्प प्रक्रम से गुजरती है तथा उसकी मोलर - ऊष्मा धारिता C स्थिर रहती है | यदि इस प्रक्रम में उसके दाब p व आयतन V के बीच सम्बन्ध नियतांक है | ( तथा क्रमशः स्थिर दाब व स्थिर आयतन पर उष्माधारिता है), तब n के लिए समीकरण है
The correct Answer is:B
बहुदैशिक प्रक्रम के लिए, आदर्श गैस की विशिष्ट ऊष्मा
(जहाँ, )
अतः मोलों की संख्या,
Topper's Solved these Questions
- ऊष्मा एवं उष्मागतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - ऊष्मा एवं उष्मागतिकी EXERCISE - बहुविकल्पीय प्रश्न II
14 Videos
- ऊष्मा एवं उष्मागतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - ऊष्मा एवं उष्मागतिकी EXERCISE - (सत्य असत्य)
6 Videos
- MOCK TEST 2022BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - MOCK TEST 2022EXERCISE - प्रश्न
18 Videos
- कार्य ऊर्जा एव सामर्थ्य BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - कार्य ऊर्जा एव सामर्थ्य EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
6 Videos
Similar Questions
एक आदर्श गैस के लिए
View Solutionसमान तापमान पर विभिन्न आदर्श गैसों के अणुओं की वर्ग - माध्य - मूल चाल समान होती है |
View Solutionमान लीजिये मुक्त आकाश (free space) में एक गोलाकार गैस के बादल का द्रव्यमान घनत्व ρ(r) है तथा इसकी केन्द्र से त्रिज्य (radial) दूरी r है I यह गैसीय बादल m द्रव्यमान के समान कणों से बना है जो कि एक समकेंद्रीय वृत्ताकार कक्षाओं में समान गतिज ऊर्जा K से घूम रहे हैं। इन कणों पर पारस्परिक गुरुत्वाकर्षण बल लग रहा है। यदि ρ(r) समय के साथ एक स्थिर राशि है, तब कणों का संख्या घनत्व n(r) = ρ(r)/m का मान होगा,
[G सार्वत्रिक गुरुत्वीय नियतांक है]
View Solutionएक नत समतल के घर्षण रहित पृष्ठ पर M द्रव्यमान का एक छोटा गुटका गतिमान है, बिंदु B पर नत समतल का कोण 60∘से 30∘ अचानक परिवर्तित होता है। गुटका प्रारम्भ में बिंदु A पर विरामावस्था में है। नत समतल तथा गुटके के बिच संघट्ट अप्रत्यास्थ माना गया (g=10मीसे2)
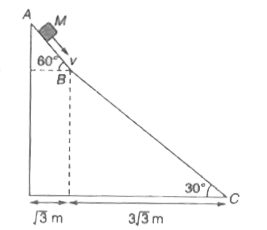
दूसरे नत समतल से टकराने के तुरंत बाद बिंदु B पर गुटके की चाल है
View Solutionवर्तिकाग्र स्त्रीकेसर के ...... में स्थिर होता है।
View Solution27^@C पर एक अभिक्रिया के लिए K_p से K_c का अनुपात 24.63 L atm mol^(-1) है। यदि नियत दाब पर अभिक्रिया की ऊष्मा 98.8 kcal है, तो नियत आयतन पर अभिक्रिया की ऊष्मा (kcal में) क्या होगी?
View Solutionनिम्नलिखित में से कोनसा आयतन (V ) और तापमान ( T ) ग्राफ एक वायुमंडलीय दाब पर एक आदर्श गैस के एक मोल के व्यवहार को दर्शाता है
View Solutionएक स्थिर आयतन ऊष्मातापी में अणुभार 28 की एक गैस के 3.5 gको 298.0K पर ऑक्सीजन के अधिवाकय में जलाया गया था दहन प्रक्रम के कारण उष्मामापी के टप्प 298.0K से 298.45 K तक की वृद्धि पायी गयी दिया हुआ है की उष्मामापी की उष्मा धारिता 2.5 kg K^-1 है गैस के दहन की अन्थेलपी का संख्यात्मक मान में है
View Solutionस्थिर दाब पर जल की मोलर ऊष्मा धारिता C_(p),75JK^(-1)"mol"^(-1) है । जब 1kg जल को 10kg ऊष्मा दी जाती है जो प्रसार के लिए मुक्त होती है तो तल के ताप में वृद्धि होगी
View Solutionएक आदर्श गैस के दस मोलों को एक बंद पात्र में भरा जाता है । पात्र में बेलन और पिस्टन के प्रकार की व्यवस्था है और 0.821 atm पर गैस का दाब स्थिर रहता है। निम्नलिखित में से कौन सा आलेख logV और logT के परिवर्तन का सही निरूपण करता है? (V= आयतन(लीटर में) और T= ताप (केलिवन में)
View Solutionआदर्श गैस के 1 मोल का आदर्श गैस समीकरण PV = nRT है। स्थिर आयतन पर P और T के बीच का वक्र, अर्थात समआयतनिक वक्र, निम्न प्रकार आरेखित है, निम्नलिखित में से आयतन का कौन सा क्रम सही है?
View Solutionनिम्न में से कौनसा आरेख स्थिर ताप पर एक आदर्श गैस के लिए β[β=−dV(dP)T/V] , P के मध्य सही परिवर्तन को प्रदर्शित करता है?
View Solution300K पर एक समतापीय प्रक्रम में, एक आदर्श गैस का 1 मोल 50 atm के बाह्य दाब के विरुद्ध 100 atm दाब से प्रसारित होता है | तब प्रक्रम में कुल एन्ट्रापी (Cal K^(-1) )
View Solutionएक आदर्श गैस 1×10Nm−2 के स्थिर दाब के विरुद्ध 300 K पर 1×10−3m3 से 1×10−2m3 तक आयतन में प्रसारित होती है। किया गया कार्य है:
View Solutionनियत आयतन पर गैस के मोलों की एक निश्चित संख्या के लिए, ताप में वृद्धि के साथ गैस का दाब किसके कारण बढ़ता है
View Solutionस्थिर आयतन पर, एक आदर्श गैस के 4 मोल को जब 300 K से 500K तक गर्म किया जाता है तो इसकी आंतरिक ऊर्जा 5000 J से परिवर्तित होती है। स्थिर आयतन पर मोलर ऊष्मा धारिता है?
View Solution
