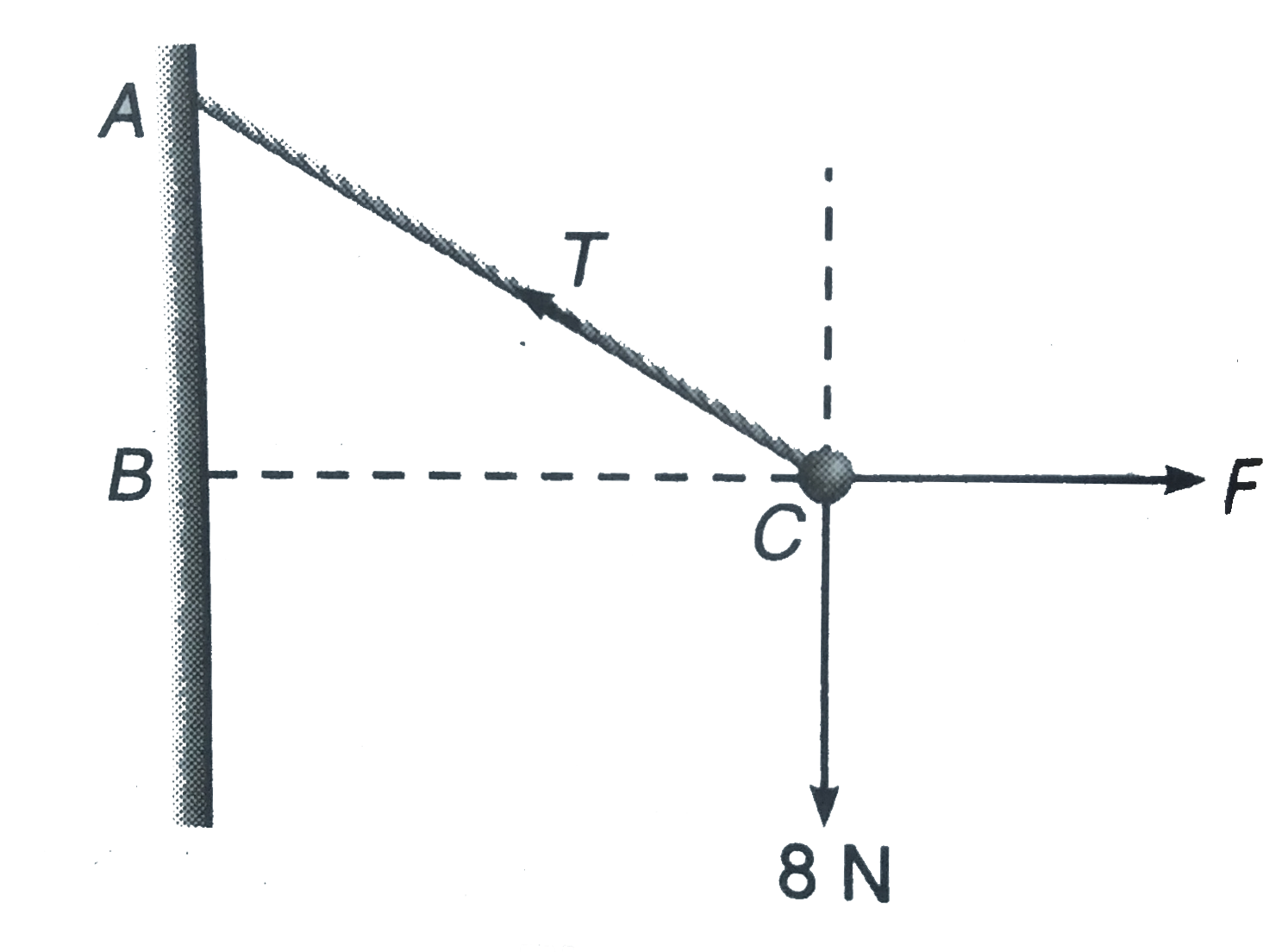
One end of a string 0.5m long is fixed to a point A and the other end is fastened to a small object of weight 8N. The object is pulled aside by a horizontal force F, until it is0.3m from the vertical through A.Find the magnitude of the tension T in the string and force F.
8N
6N
2N
1N
The correct Answer is:B
AC=0.5 m, BC=0.3 m,
∴AB=0.4m
and if ∠BAC=θ
Then , cosθ=ABAC=0.40.5=45
and sinθ=BCAC=0.30.5=35

Here, the object is in equilibrium under three concurrent forces. So, we can apply Lami, therorem.
or Fsin(180∘−θ)=8sin(90∘+θ)=Tsin90∘
or Fsinθ=8cosθ=T
∴T=8cosθ=84/5=10N and F=8sinθcosθ=(8)(3/5)(4/5)=6N
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.120videos
LAWS OF MOTION
- BOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.215videos
LAWS OF MOTION
- BOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Subjective Question27videos
LAWS OF MOTION
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
- BOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective18videos
LAWS OF THERMODYNAMICS
Similar Questions
A stone with a mass of 0.9 kg is attached to one end of a string 0.8 m long. The string will break if its tension exceeds 500 N. The stone is whirled in a horizontal circle on a frictionless table top. The other end of the string is kept fixed. Find the maximum speed of the stone, it can attain without breaking the string.
View SolutionOne end of a string of length 1.5 m is tied to a stone of mass 0.4 kg and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at its lower most point so that the string does not slack at any point in its motion along the vertical circle ?
View Solution
Knowledge Check
- Question 1 - Select One
A body of mass √3 kg is suspended by a string to rigid support.The body is pulled horizontally by a force F until the string makes an angle of 30∘ with the vertical.The value of F and tension in the string are
A9.8N,9.8NB9.8N,19.6NC19.6N,19.6ND19.6N,9.8N - Question 2 - Select One
One end of string of length l is connected to a particle on mass m and the other end is connected to a small peg on a smooth horizontal table. If the particle moves in circle with speed v the net force on the particle (directed toward centre) will be (T reprents the tension in the string):
AT+mv21BT−mv21CzeroDT - Question 3 - Select One
One end of string of length / is connected to a particle of mass 'm' and the other end is connected to a small peg on a smooth horizontal table. If the particle moves in circle with speed 'v', the net force on the particle (directed towards centre) will be (T represents the tension in the string)
AT+mv2lBT−mv2lCzeroDT
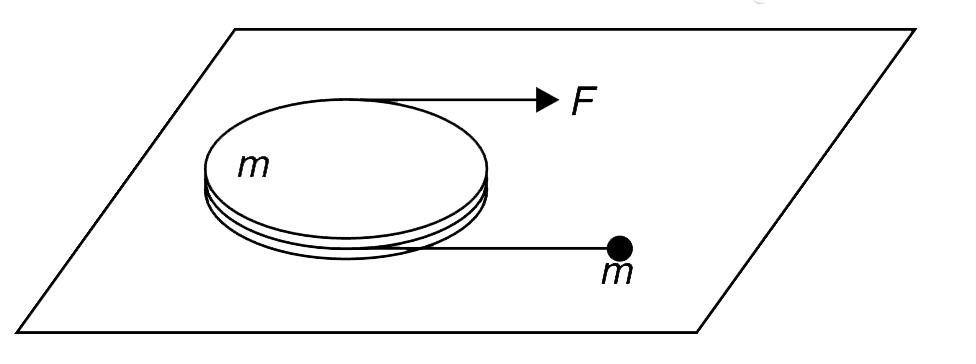
A disc of mass m lies flat on a smooth horizontal table. A light string runs halfway around it as shown in figure. One end of the string is attached to a particle of mass m and the other end is being pulled with a force F. There is no friction between the disc and the string. Find acceleration of the end of the string to which force is being applied.
 View Solution
View SolutionA uniform string of length 6.5m is subjected to a tension of 40N. Mass of the string is 162.5g. One end of the string is fixed and the other end is tied to a source (s). which produces a transverse oscillation. The displacement of the end of the string tied to the source can be expressed as y=(3mm)sin(40πt), where ‘t’ is time. Find the displacement of point P of the string at a distance of 3.75m from the fixed end, at time t=0.3s.
 View Solution
View SolutionA uniform thick string of length 5 m is resting on a horizontal frictionless surface. It is pulled by a horizontal force of 5 N from one end. The tension in the string at 1m from the force applied is :
View SolutionIn the figure a rope of mass m and length l is such that its one end is fixed to rigid wall and the other is applied with a horizontal force F as shown below, then tension at the middle of the string is:
 View Solution
View SolutionIf one end of a wire is fixed with a rigid support and the other end is stretched by a force of 10 N, the increase in length is 0.5 mm. The ratio of enegry of the wire and the work done in displacing it through 1.5 mm by the weight is
View Solution

