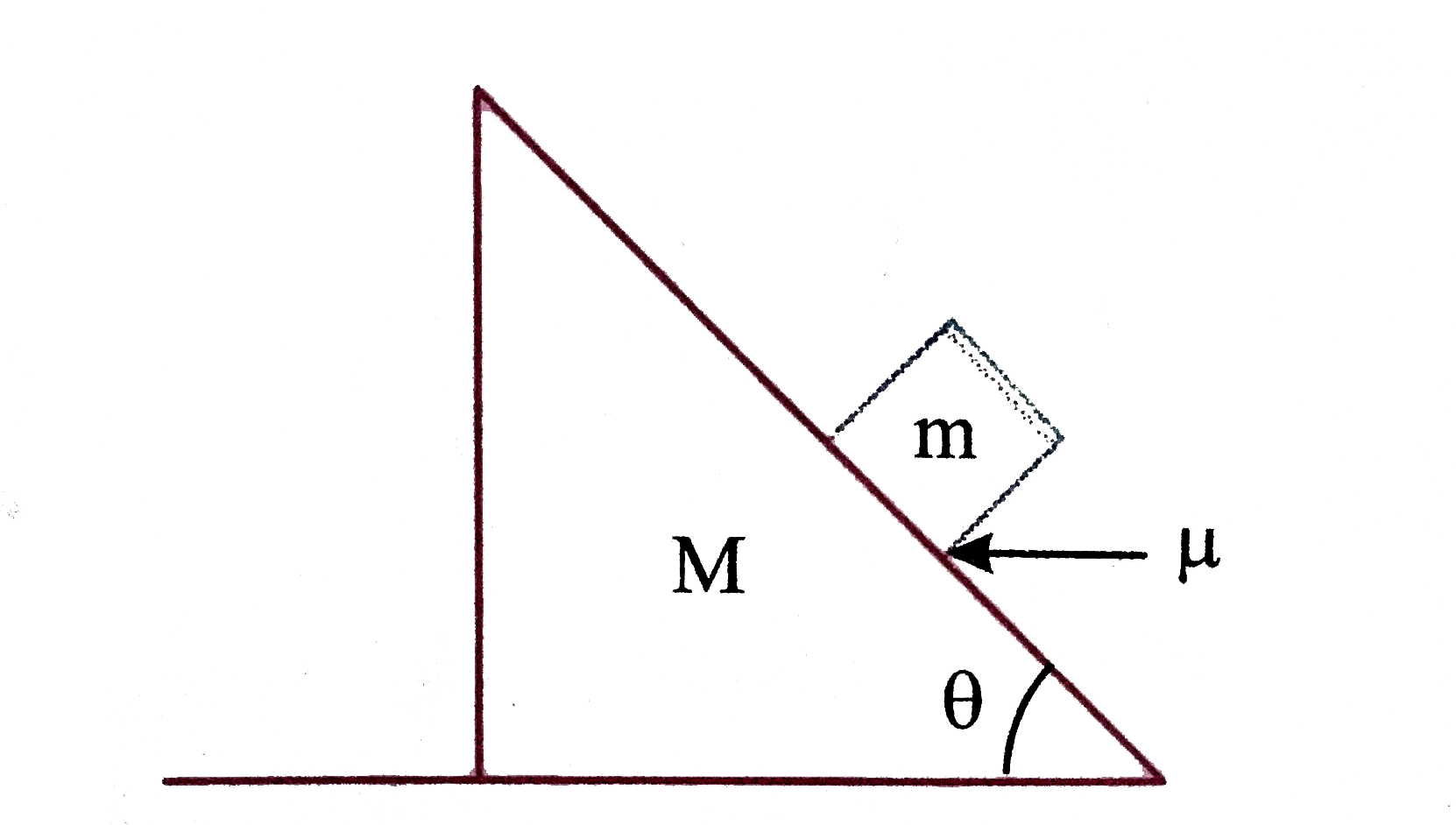
A wedge of mass 2m and a cube of mass m are shown in figure. Between cube and wedge, there is no friction. The minimum coefficient of friction between wedge and ground so that wedge does not move is:

0.1
0.2
0.3
0.4
The correct Answer is:B
(b)a=gsinθ=g√2

aH=aV=g√2×1√2=g2
N√2=mg2…….(i)
mg−N√2=mg2……(ii)
N'=N√2+2mg……(iii)
μN'=N√2…….(iv)

Solving above four equations, we get
μ=0.2
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Assertion and reason
28 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.4
20 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
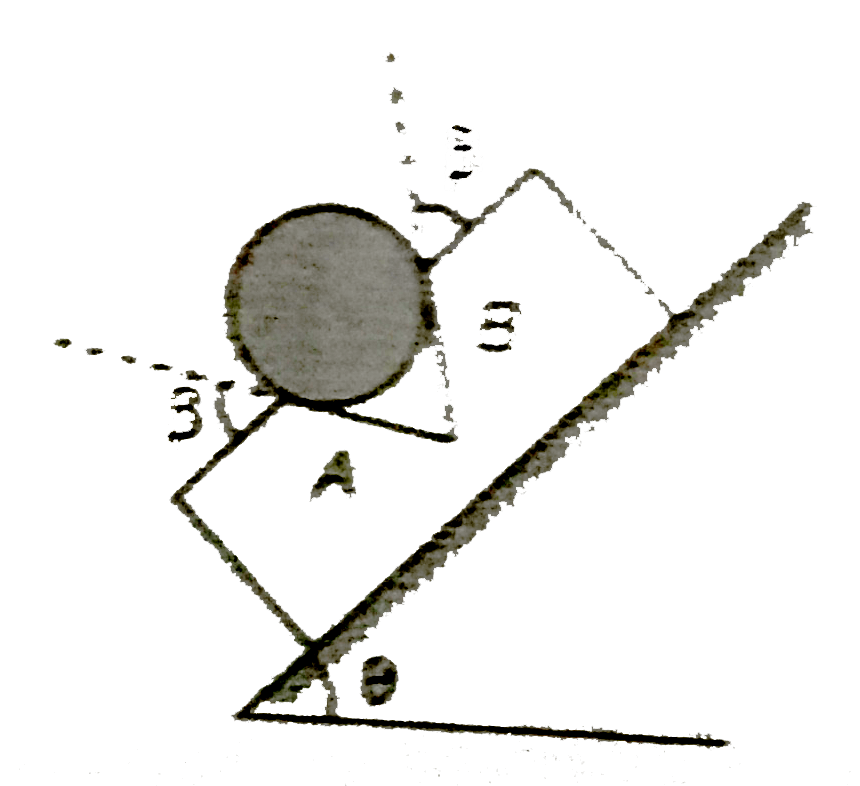
A block of mass m lies on wedge of mass Mas shown in figure. Find the minimum friction coeffcient required between wedge Mand ground so that it does not move while block m slips down on it.
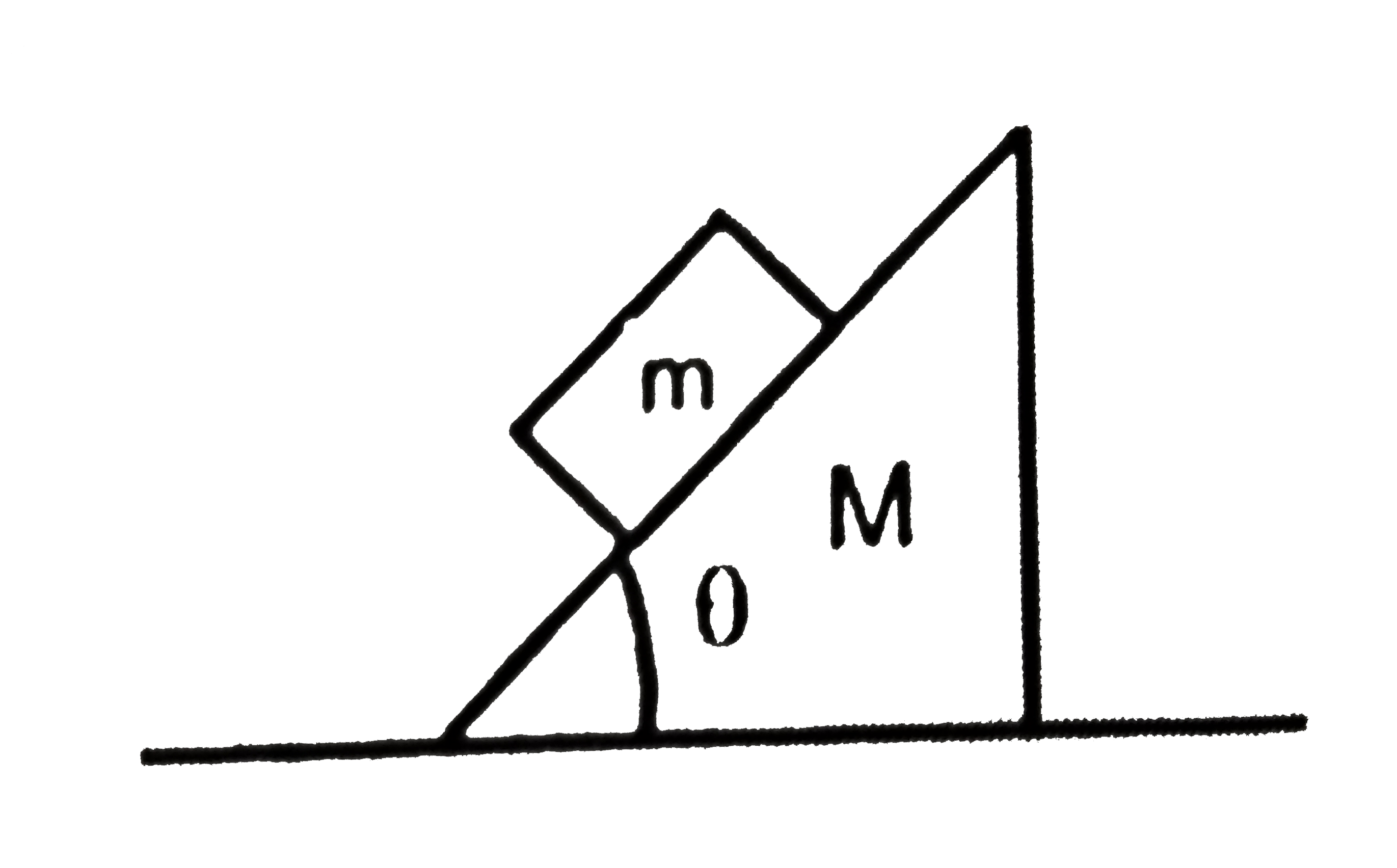
View SolutionTwo small blocks of mass mA=30 kg & mB =15 kg are connected with spring & kept on the wedge which is rotating about given axis as shown in figure. If blocks B remain in rest then minimum value of coefficient of friction between block A & wedge is μ0, then the value of μ20 is :
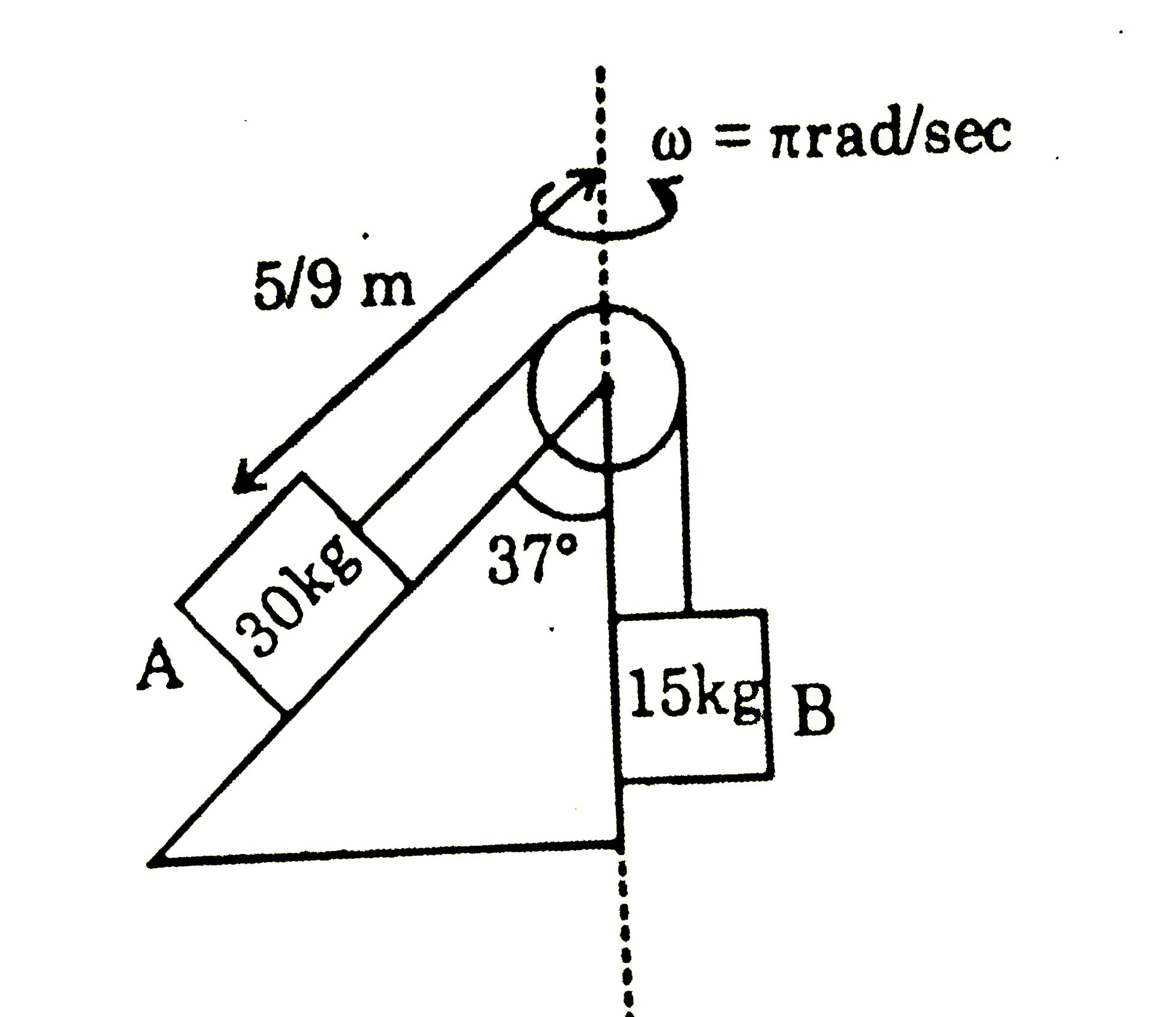
View Solution
Knowledge Check
a Block of mass m is placed on a wedge of mass M there is no friction between the block and the wedge .The minmum coefficient of friction between the wedge and the gound so that wedge does not move is,
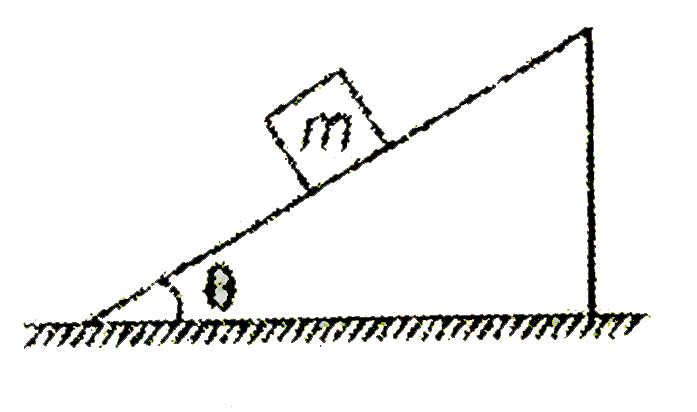 Amcos2θM+mcos2θBmsin2θM+mcos2θCmcosθsinθM+mcos2θDmcosθsinθM+msin2θ
Amcos2θM+mcos2θBmsin2θM+mcos2θCmcosθsinθM+mcos2θDmcosθsinθM+msin2θA cube of mass m is placed on top of a wedge of mass 2m, as shown in figure. There is no friction between the cube and the wedge. The minimum co - efficient of friction between the wedge and the horizontal surface, so that the wedge does not move is
 A0.1B0.2C0.3D1√2
A0.1B0.2C0.3D1√2The air of density ρ and moving with a velocity v strikes perpendicular the inclined surface of area A and of a wedge kept on a horizontal surface. The mass of the wedge is m. Assuming the collisions to be perfectly inelastic, the minimum value of the coefficient of friction between the wedge and the ground so that the wedge does not move is (Assume mass of particles of air is negligible)
 AρAv2sinθmg+ρAv2cosθBtanθCρAv2mgtanθDρAv2mg+ρAv2cosθ
AρAv2sinθmg+ρAv2cosθBtanθCρAv2mgtanθDρAv2mg+ρAv2cosθ
A block of mass mlies on wedge of mass M as shown in figure. Answer following parts separately. (a)Withwhat minium acceleration must the wedge be moved towards right horizontally so that block m falls freely.

( b)Find the minimum friction coefficient required between wedge M and ground so that it does not move while block m slips down on it.
View SolutionA block of mass 2 kg is kept on a smooth wedge of mass 3 kg and wedge is kept on a rough horizontal surface. A vertical force of 60 N is applied on the minimum coefficient of friction between the wedge and horizontal surface, so that wedge remains at rest during the motion of block on the wedge ?
View SolutionA block of mass 1 kg is placed on a wedge shown in figure. Find out minimum coefficient of friction between wedge and block to stop the block on it.

View SolutionCalculate angle of friction between wedge and block system is at rest M coefficient of friction between wedge and block.
View SolutionTwo wedges, each of mass m, are placed next to each other on a flat horizontal floor. A cube of mass M is balanced on the wedges as shown in figure. Assume no friction between the cube and the wedges, but a coefficent of static friction μ<1 between the wedges and the floor. What is the largest M that can be balanced as shown without motion of the wedges ?

View Solution
