Imagine a narrow tunnel between the two diametrically opposite points of the earth. A particle of mass m is released in this tunnel . The time period of oscillation is
π√Rg
π2√Rg
2π√Rg
2π√Rg
The correct Answer is:C
To find the time period of oscillation for a particle of mass m released in a tunnel that goes through the Earth, we can follow these steps:
Step 1: Understand the System
The particle will oscillate back and forth through the tunnel due to gravitational force. When it is at the center of the Earth, the gravitational force acting on it will be zero, and it will experience a restoring force when it moves away from the center.
Step 2: Use the Concept of Simple Harmonic Motion (SHM)
The motion of the particle can be modeled as simple harmonic motion (SHM). In SHM, the time period T is given by the formula:
T=2π√lg
where l is the effective length of the pendulum and g is the acceleration due to gravity.
Step 3: Determine the Effective Length
In this case, the effective length l is the radius of the Earth R. Therefore, we can substitute l with R:
T=2π√Rg
Step 4: Substitute Known Values
Here, R is the radius of the Earth (approximately 6.4×106 meters) and g is the acceleration due to gravity (approximately 9.81m/s2). However, we do not need to substitute the actual values since the question only asks for the expression for the time period.
Final Expression
Thus, the time period of oscillation of the particle in the tunnel through the Earth is:
T=2π√Rg
The particle will oscillate back and forth through the tunnel due to gravitational force. When it is at the center of the Earth, the gravitational force acting on it will be zero, and it will experience a restoring force when it moves away from the center.
The motion of the particle can be modeled as simple harmonic motion (SHM). In SHM, the time period T is given by the formula:
T=2π√lg
where l is the effective length of the pendulum and g is the acceleration due to gravity.
In this case, the effective length l is the radius of the Earth R. Therefore, we can substitute l with R:
T=2π√Rg
Here, R is the radius of the Earth (approximately 6.4×106 meters) and g is the acceleration due to gravity (approximately 9.81m/s2). However, we do not need to substitute the actual values since the question only asks for the expression for the time period.
Thus, the time period of oscillation of the particle in the tunnel through the Earth is:
T=2π√Rg
Similar Questions
Asume that as narrow tunnel is dug between two diametricaly opposite points of the earth. Treat the earth as a solid sphere of uniform density. Show that ilf a particle is relesed in this tunel, ilt wil execute a simple harmonic motion. Calculate the time period of this motion.
View SolutionA particle in a circular path speeds up with a uniform rate between two diametrically opposite points of a circle of radius R. If its time of motion between these two points is equal to T, find the accelertaion of the particle averaged over the time T.
View Solution
Knowledge Check
- Question 1 - Select One
The time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A2π√m6kB2π√11m6KC2π√6m11KD2π√mK - Question 2 - Select One
A particle of mass m is released from rest and follows a particle as a function of time?
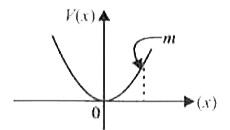 A
A B
B C
C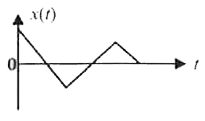 D
D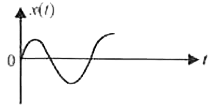
- Question 3 - Select One
A tunnel has been dug through the centre of the earth and a ball is released in it. It executes S.H.M. with time period
A42 minutesB1 dayC1 hourD84.6 minutes
A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionA tunnel has been dug through the centre of the earth and a ball is released in it. It executes S.H.M. with time period
View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.
 View Solution
View SolutionA block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is
 View Solution
View SolutionInitial angular velocity of a circular disc of mass M is ω1. Then two small spheres of mass m are attached gently to two diametrically opposite points on the edge of the disc. What is the final angular velocity of the disc -
View Solution

