Asume that as narrow tunnel is dug between two diametricaly opposite points of the earth. Treat the earth as a solid sphere of uniform density. Show that ilf a particle is relesed in this tunel, ilt wil execute a simple harmonic motion. Calculate the time period of this motion.
To solve the problem of a particle released in a tunnel dug through the Earth, we will follow these steps:
Step 1: Understanding the Setup
We assume the Earth is a solid sphere of uniform density. If a particle is released in a tunnel that connects two diametrically opposite points, it will experience gravitational force directed towards the center of the Earth.
Step 2: Gravitational Force Inside the Earth
According to Gauss's law for gravity, the gravitational force acting on a particle inside a uniform spherical shell is only due to the mass of the sphere that is at a radius less than the distance from the center to the particle. If the particle is at a distance x from the center, the gravitational force F acting on it can be expressed as:
F=−GMxmx2
where Mx is the mass of the sphere of radius x, m is the mass of the particle, and G is the universal gravitational constant.
Step 3: Mass Inside Radius x
The mass Mx can be calculated using the density ρ of the Earth:
Mx=ρ⋅43πx3
Since the density ρ is uniform, we can express it in terms of the total mass M of the Earth and its radius R:
ρ=M43πR3
Substituting this into the expression for Mx:
Mx=M43πR3⋅43πx3=M⋅x3R3
Step 4: Substituting Mx into the Force Equation
Now substituting Mx back into the force equation:
F=−G⋅M⋅x3R3⋅mx2=−GMmR3x
Step 5: Identifying Simple Harmonic Motion
This force can be compared to Hooke's law, F=−kx, where k=GMmR3. This indicates that the motion of the particle is indeed simple harmonic motion (SHM) with the restoring force proportional to the displacement x from the equilibrium position (the center of the Earth).
Step 6: Calculating the Time Period
The time period T of SHM is given by:
T=2π√mk
Substituting k:
T=2π√mGMmR3=2π√R3GM
Step 7: Final Calculation
Using the known values for G and M (mass of the Earth), and R (radius of the Earth), we can calculate T:
T≈2π
⎷(6.371×106)3(6.674×10−11)(5.972×1024)≈84.6 minutes
Summary
Thus, a particle released in the tunnel will execute simple harmonic motion with a time period of approximately 84.6 minutes.
---
We assume the Earth is a solid sphere of uniform density. If a particle is released in a tunnel that connects two diametrically opposite points, it will experience gravitational force directed towards the center of the Earth.
According to Gauss's law for gravity, the gravitational force acting on a particle inside a uniform spherical shell is only due to the mass of the sphere that is at a radius less than the distance from the center to the particle. If the particle is at a distance x from the center, the gravitational force F acting on it can be expressed as:
The mass Mx can be calculated using the density ρ of the Earth:
Now substituting Mx back into the force equation:
This force can be compared to Hooke's law, F=−kx, where k=GMmR3. This indicates that the motion of the particle is indeed simple harmonic motion (SHM) with the restoring force proportional to the displacement x from the equilibrium position (the center of the Earth).
The time period T of SHM is given by:
Using the known values for G and M (mass of the Earth), and R (radius of the Earth), we can calculate T:
⎷(6.371×106)3(6.674×10−11)(5.972×1024)≈84.6 minutes
Thus, a particle released in the tunnel will execute simple harmonic motion with a time period of approximately 84.6 minutes.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective 1
21 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
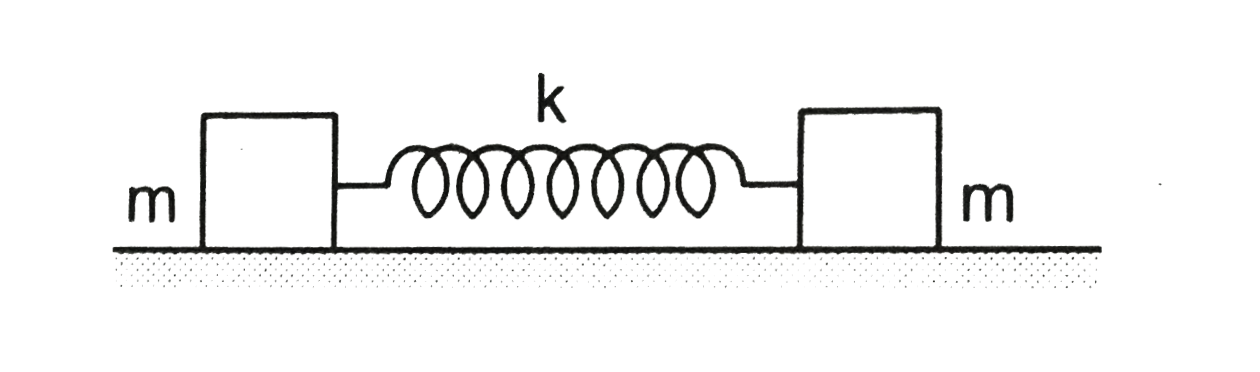
Consider the situastion shown in figure. Show that if that blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.
View SolutionA tunnel is dug through the centre of the earth. Shwo that a body of mass m when dropped form rest from one end of the tunnel will execute simple harmonic motion.
View Solution
Knowledge Check
Imagine a narrow tunnel between the two diametrically opposite points of the earth. A particle of mass m is released in this tunnel . The time period of oscillation is
Aπ√RgBπ2√RgC2π√RgD2π√RgAssume that a tunnel is dug along a chord of the earth, at a perpendicular distance (R/2) from the earth's centre, where 'R' is the radius of the Earth. The wall of the tunnel is frictionless. If a particle is released in this tunnel, it will execute a simple harmonic motion with a time period :
A2πRgBg2πrC12π√grD2π√RgIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Time period of the particle is not equal toA2π√RgB2π√GMR3/2C84.6 minDNone of these
A short , straight and frictinless tunnel is bored through the centre of the earth and a body is realesed from the surface into the tunnel . Show that the motion of the body in the tunnell will be simple harmoic and hence calculate the taken by the body to travel from one end of the tunnel to the other (Radius of the earth = 6.38×106m and acceleration due to gravity at the surface = 9.81ms2
View SolutionTwo points charges , each Q , are fixed at separation 2d. A charged particle having charge q and mass m is placed between them.
(a) Now this charged particle is slightly displaced along the line joining the charges , slow that it will execute simple harmonic motion and find the time period of oscillation.
(b) If charge q is negative and it is displaced slightly perpendicular to the line joining the charges , repeat the part (a).
View SolutionA spring of force constant k and negligible mass is attached to a rigid mass m at one end and clamped to a strong support at the other. The mass is displaced a little and then released. Show that the body executes simple harmonic motion and calculate its time period. If the spring is cut into three equal pieces and the same body is supported by one such piece in a smaller way, by how much will the time period be increased or decreased?
View SolutionThe figure shows graph between velocity 'V' and displacement 'X' from mean position of a particle performing simple harmonic motion

The time period of motion of particle is:
View Solution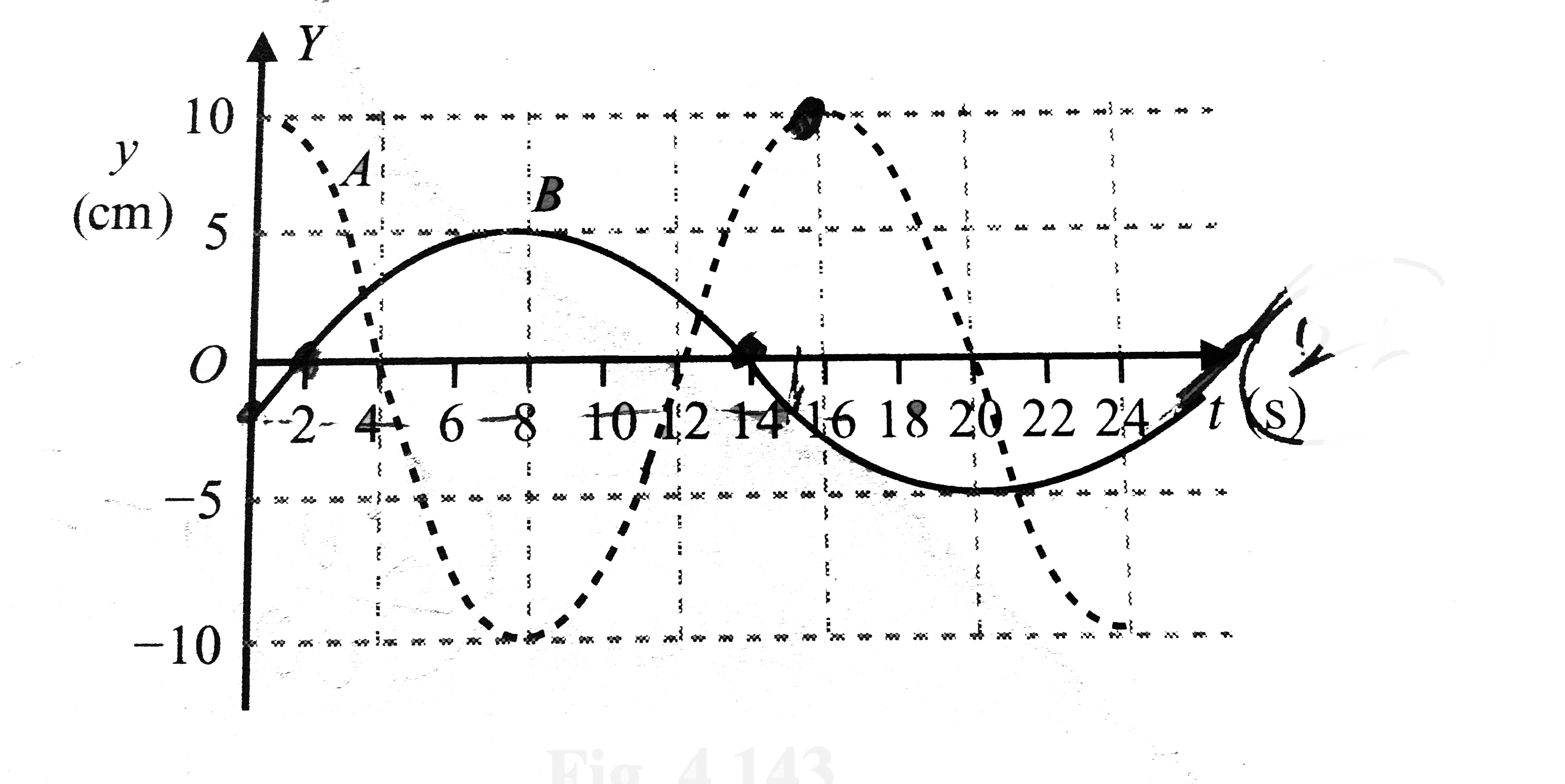
The following figure shows the displacement versus time graph for two particles A and B executing simple harmonic motions. The ratio of their maximum velocities is
View Solution
