The bulk modulus of an ideal gas at constant temperature
is equal to its volume V
is equal to p/2
is equal to its pressure p
Cannot be determined
The correct Answer is:C
(d) Bulk modulus, B=p−ΔVV⇒B=hρg0.1×10−2
⇒ Depth, h=B×0.1×10−2ρg=9×108×0.1×10−2103×10=90m
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Check point 12.3
15 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Chapter Exercise
73 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Check point 12.1
15 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
434 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
Knowledge Check
For a certain amount of an ideal gas at constant temperature, __________________.
Avolume always remains constantBpressure always remains constantCproduct of pressure and volume remains constant.Dthe ratio of pressure and volume always remains constant.For given mass of an ideal gas at constant temperature
AP vs V graph is a straight line passing through originBP vs 1V graph is a rectangular hyperbolaCPV vs P graph is a straight line passing through originDPV vs V graph is a straight lineWhich of the following curve is incorrect for given amount of an ideal gas at constant temperature ?
A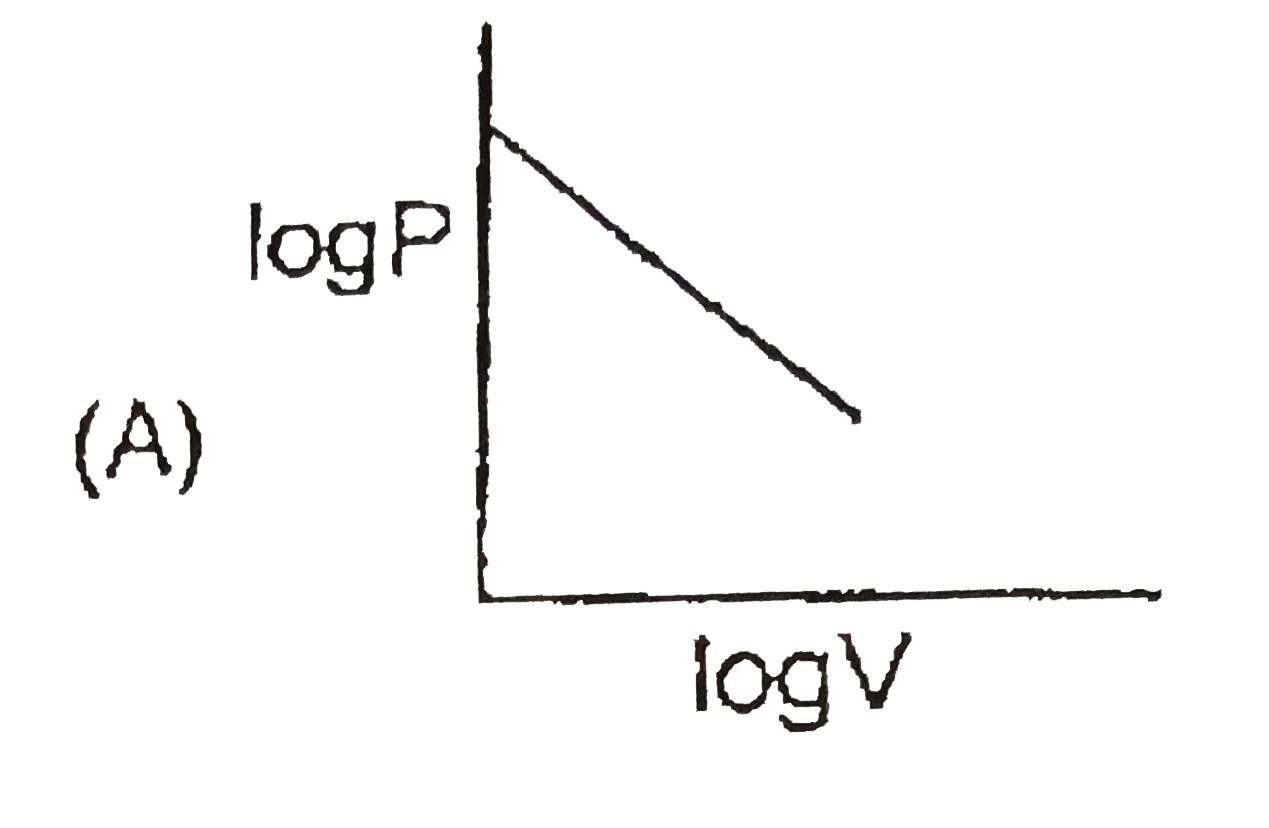 B
B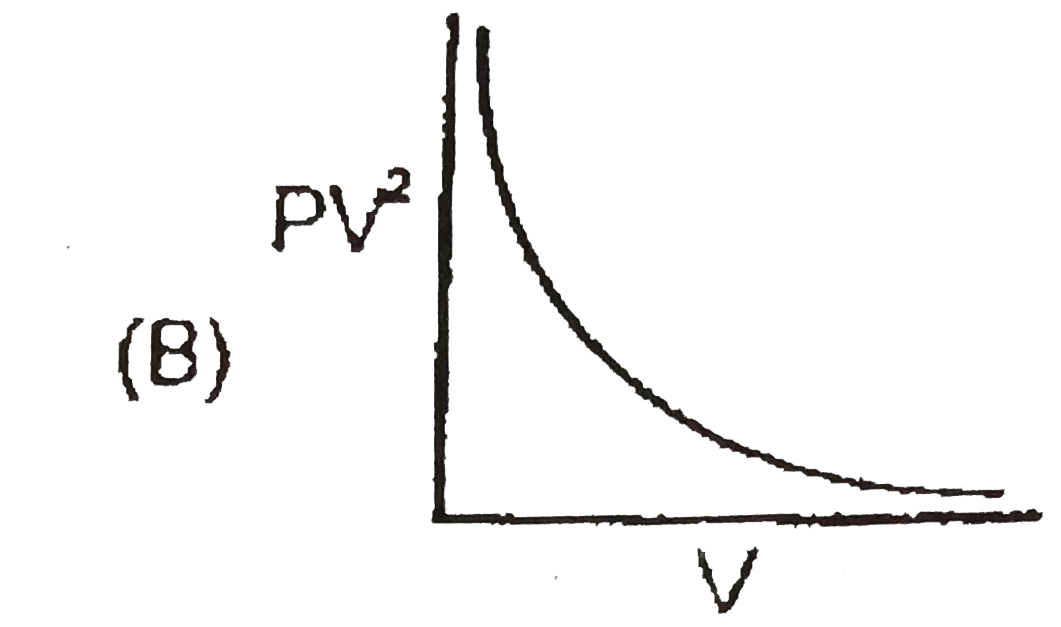 C
C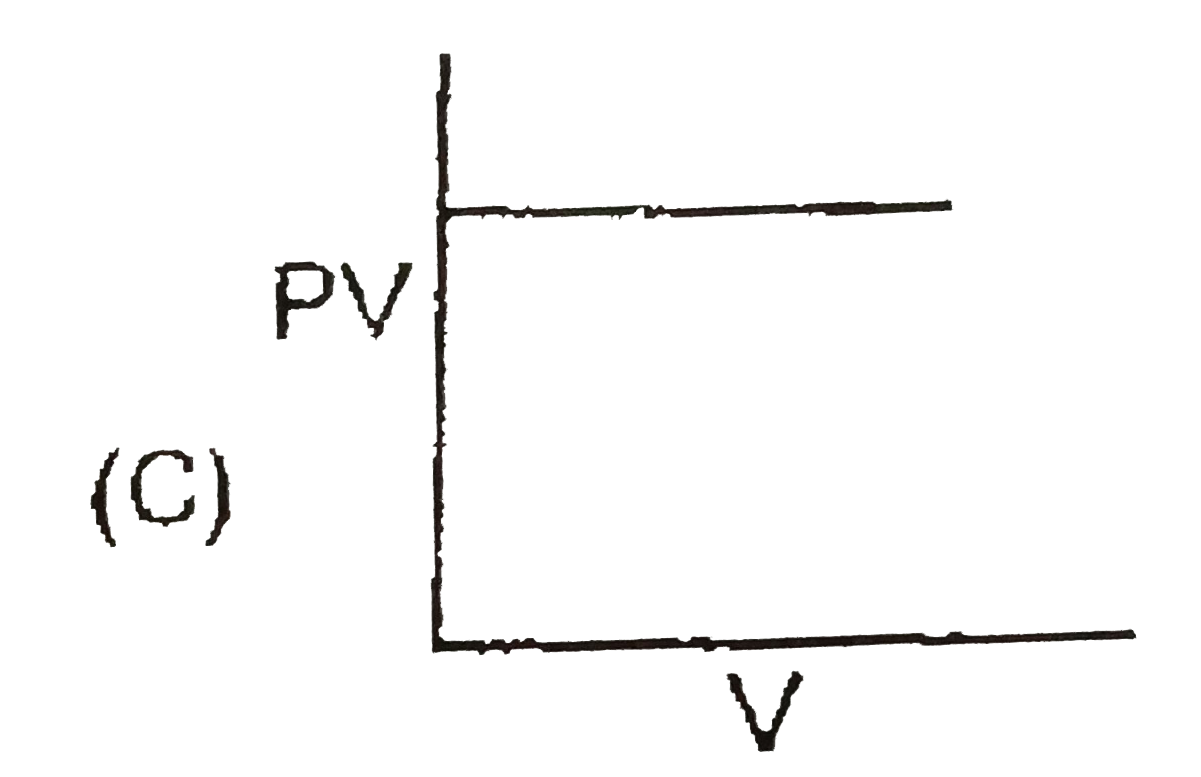 D
D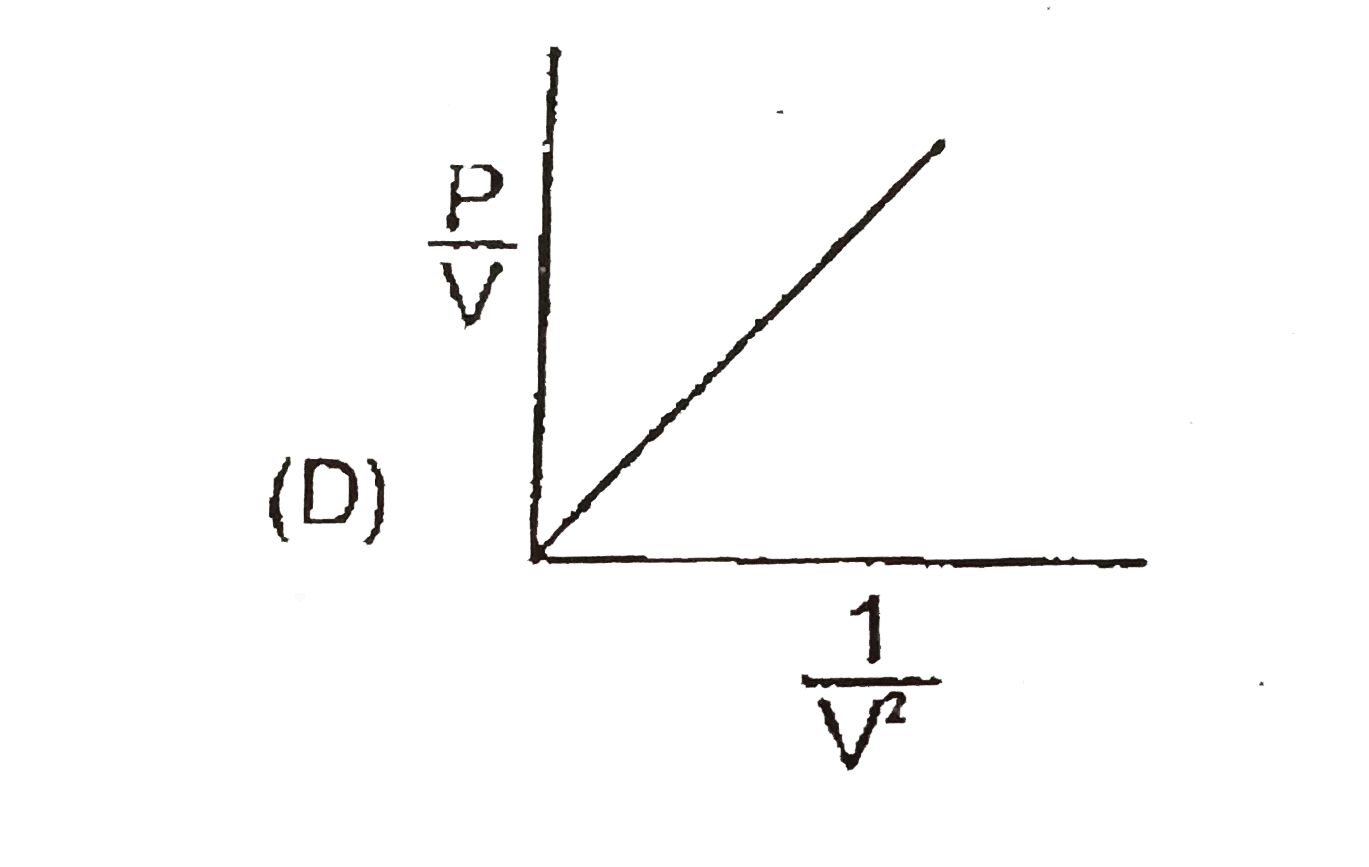
There is no change in internal energy for an ideal gas at constant temperature.
Internal energy of an ideal gas is a function of temperature only.
View SolutionThe isothermal Bulk modulus of an ideal gas at pressure P is
View SolutionThe raise in the temperature of a given mass of an ideal gas at constant pressure and at temperature 27∘ to double its volume is
View SolutionOne mole of an ideal gas at an initial temperature true of TK does 6R joule of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is 5/3, the final temperature of the gas will be
View SolutionOne mole of an ideal gas at an initial temperature true of TK does 6R joule of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is 5/3, the final temperature of the gas will be
View Solution
