Under isothermal condition two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r. The external pressure is p0. Find the surface tension of the soap in terms of the given parameters.
2p0(r3−r31−r32)4(r21+r22−r2)
p0(r3−r31−r32)4(r21+r22−r2)
p0(r3+r21+r32)4(r21+r22+r2)
None of these
The correct Answer is:B
As mass of the air is conserved,
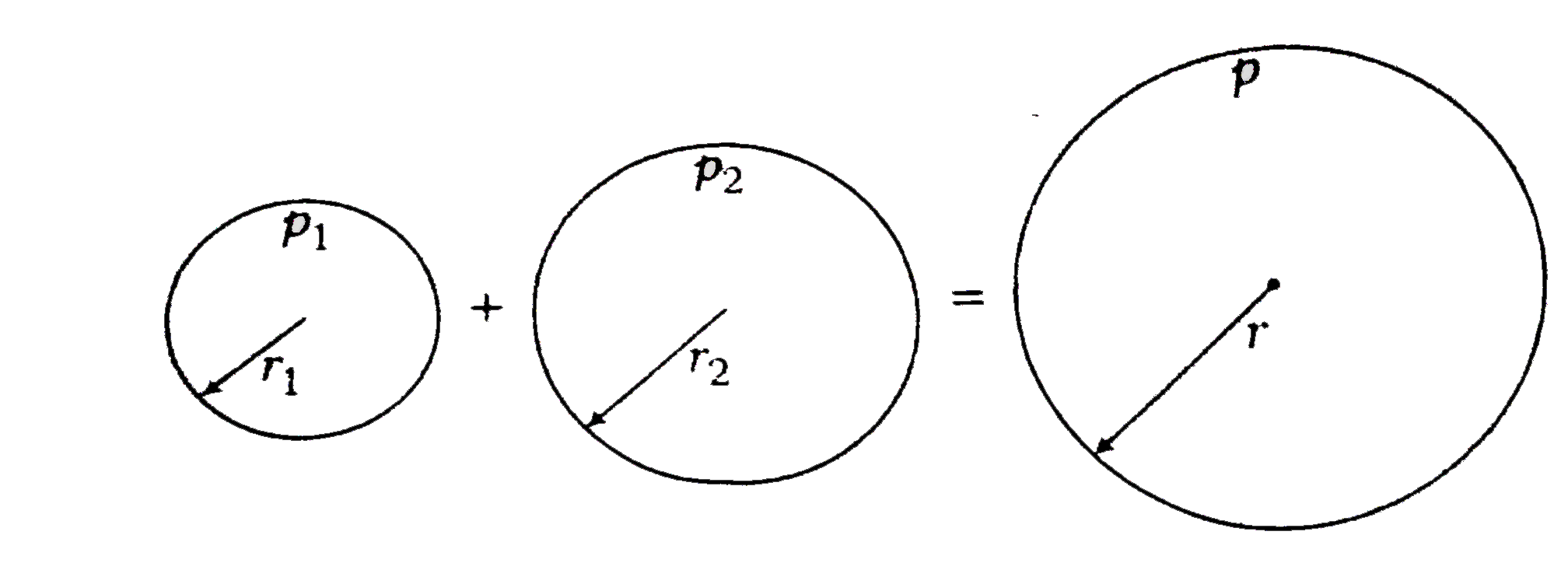
∴ n1+n2=n (aspV=nRT)
∴p1V1RT1+p2V2RT2=pVRT
As temperature is constant,
T1=T2=T
∴p1V1+p2V2=pV
∴(p0+4Sr1)(43πr31)+(p0+4Sr2)(43πr32)=(p0+4Sr)(43πr3)
Solving, this we get
S=p0(r3−r31−r32)4(r1r2+r22−r2)
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question19videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Match the columns6videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.410videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
Two soap bubbles of radii a and b coalesce to form a single bubble of radius c. If the external pressure is P, find the surface tension of the soap solution.
View SolutionTwo soap bubble of radii r1 and r2 combime to form a single bubble of radius r under isothermal conditions . If the external pressure is P, prove that surface tension of soap solution is given by S=P(r3−r31−r32)4(r21+r22−r2).
View Solution
Knowledge Check
- Question 1 - Select One
Two soap bubbles of radii R1andR2 kept in atmosphere are combined isothermally to form a big bubble of radius R. The expression for surface tension will be
AP0(R3+R31+R32)4(R2+R21+R22)BP0(R31+R32−R3)4(R2−R21−R22)CP0(R31+R32−R3)D4P0(R31+R32−R3) - Question 2 - Select One
Prove that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
Ar2−r1Br2−r1r1r2Cr1r2r2−r1Dr2+r1 - Question 3 - Select One
When two soap bubbles coalesce to form a single bubble then its radius will be-
A0B∞Cr2D√2r
Find the work done in blowing a soap bubble of radius R if pressure outside in p0 and the surface tension of the soap solution is T.
View SolutionTwo soap bubbles of radii a and b coalesce to form a single bubble of radius c. If the external pressure is P, show that the surface tension T is given by T=Pc3−a3−b34(a2+b2−c2)
View SolutionTwo soap bubbles of radius R1 and R2 combine isothermally to form a new soap bubble. Find radius of new soap bubble
View SolutionFind the work to be performed in order to blow a soap bubble of radius R if the outside air pressure is equal to p0 and the surface tension of the soap water solution is equal to α.
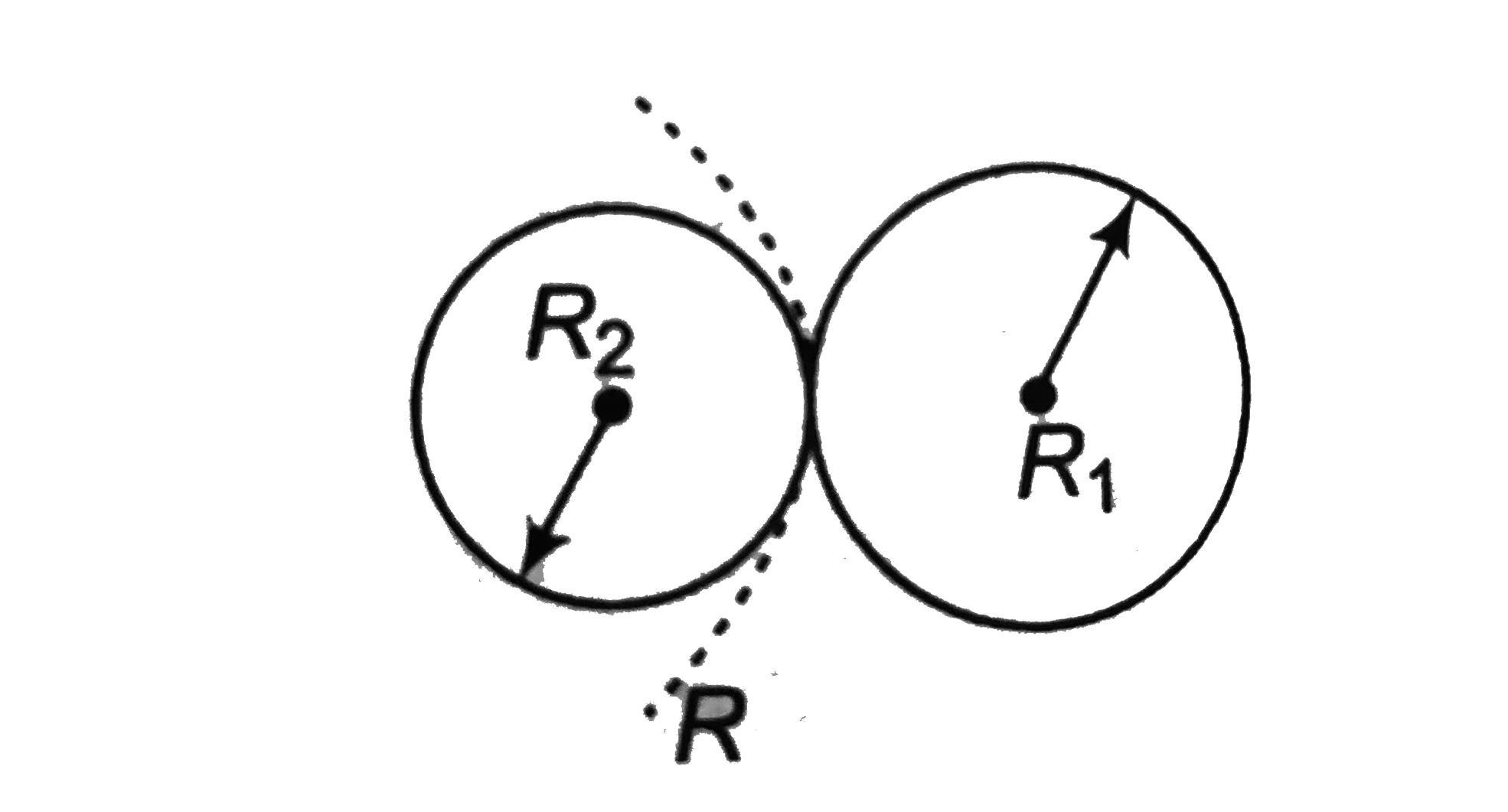
View SolutionTwo soap bubble of different radii R1 and R2(<R1) coalesce to form an interface of radius R as shown in figure. The correct value of R is
 .View Solution
.View Solution

