An aluminium cylinder 10 cm long. As a spacer between two steel walls. At 12∘C it juct slips in between the walls. When it warms to 23∘C calculate the stress in the chlinder and the total force it exerts on each wall, assuming that the walls are perfectly rigid and a constant distance apart.
Given, For aluminium Y=7.0×10−10 Pa and α=2.4×10−5K−1
Change in temperature, ΔT=5.1∘C=5.1K
Area A =20cm2=20×10−4m2
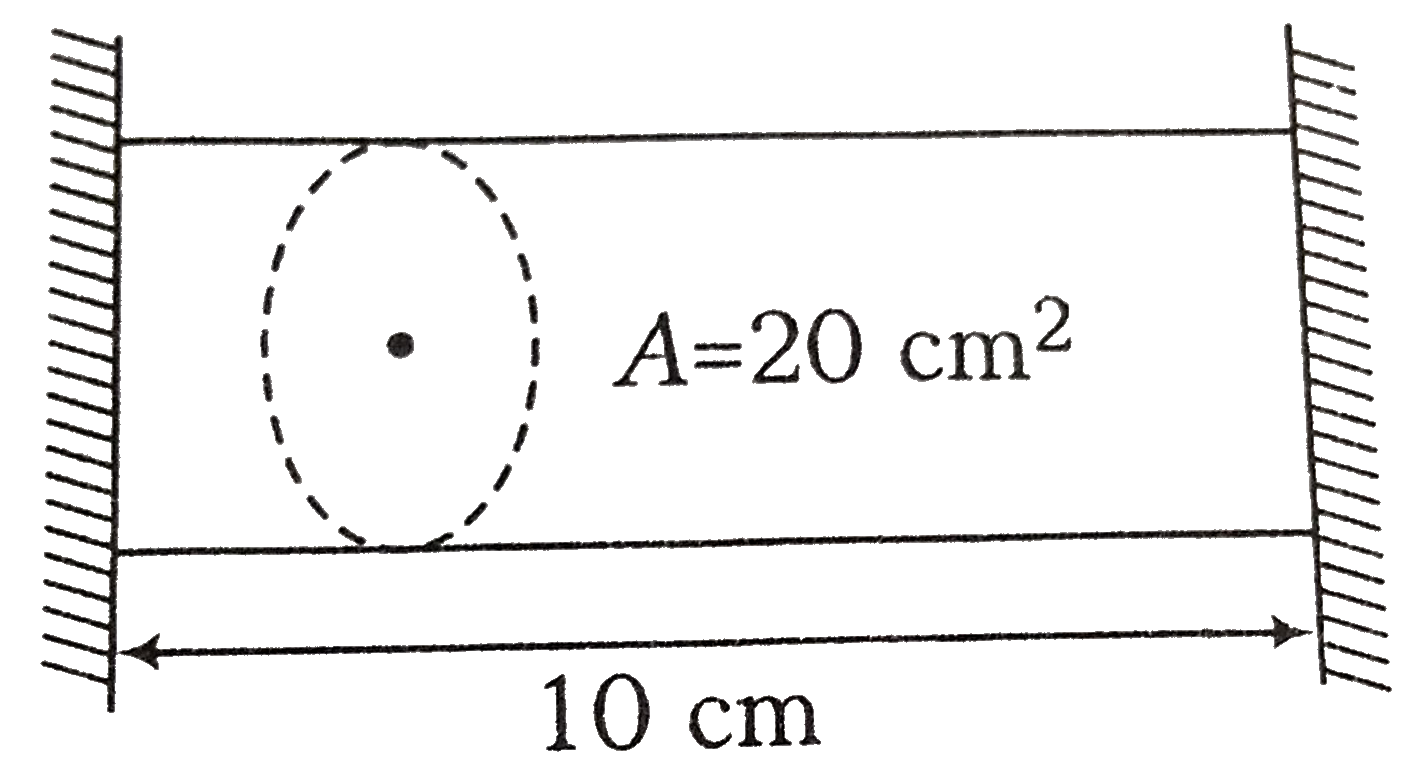
∴Stress=FA=YαΔT=(0.70×1011Pa)(2.4×10−5K−1)(5.1K)
=1.68×5.1×106=8.6×106 Pa
The total forcr F is the cross-seactional times thje stress.
F=stress xx area =(8.6×106Pa)(20×10−4m2)=1.7×104N
Topper's Solved these Questions
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEYCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Check point 14.1
10 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEYCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Check point 14.2
20 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEYCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEYCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Subjective
9 Videos
Similar Questions
An aluminum cylinder 10 cm long with a cross section area of 20cm2 is used as a spacer between two steel walls. At 17.2∘C it just slips in between the walls. When it warms to 22.3∘C calculate the stress in the cylinder and the total force it exerts on each wall, assuming that the walls are perfectly rigid and a constant distance apart.
View SolutionAn aluminium cylinder 10 cm long, with a cross-sectional area of 20cm2, is to be used as a spacer between two steel walls. At 17.2∘C it just slips in between the walls. When it warms to 22.3∘C, calculate the stress in the cylinder and the total force if exerts on each wall, assuming that the walls are perfectly rigid and a constant distance apart.
View Solution
Knowledge Check
A ladder 5m long rests against a vertical wall. If its top slides down at the rate of 10cm/sec, then, when the foot of the ladder is 4m away from the wall, the angle between the floor and the ladder is decreasing at the rate of
Aπ4radians/sec.B4πradians/sec.C(0.025)radians/sec.Dπ6radians/sec.
Two identical spheres of radii 10 cm each are placed in between two rigid walls (vertical) as shown. The spacing between the walls is 36 cm. Then find the force of contact between the spheres, if the weight of each sphere is 'W'.
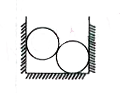
View SolutionA particle of mass m is trapped between two perfectly rigid parallel walls. The particle bounces back and forth between the walls without losing any energy. From a wave point of view, the particle trapped between the walls is like a standing wave in a stretched string between the walls. Distance between the two walls is L.
(a) Calculate the energy difference between third energy state and the ground state (lowest energy state) of the particle.
(b) Calculate the ground state energy if the mass of the particle is m=1mg and separation between the walls is L=1cm.
View SolutionFigure shows a steel rod of cross sectional ara 2×10−6m2 is fixed between two vertical walls. Initially at 20∘C there is no force between the ends of the rod and the walls. Find the force which the rod will exert on walls at 100∘C. Given that the coefficient of linear expansion of steel is 1.2×10−5.∘C−1 and Young's modulus is 2×1011N/m2

View SolutionTwo large rigid vertical walls A and B are parallel to each other and separated by 10m. A particle of mass 10g is projected with an initial velocity of 20m/s at 45∘ to the horizontal from point P on the ground, such that AP=5m. The plane of motion of the particle is vertical and perpendicular to the walls. Assuming that all the collisions are perfectly elastic, find the maximum height attained by the particle and the total number of collisions suffered by the particle with the walls before it hits ground. Take g=10m/s2.

View SolutionTwo large rigid vertical walls A and B are parallel to each other and separated by 10m. A particle of mass 10g is projected with an initial velocity of 20m/s at 45∘ to the horizontal from point P on the ground, such that AP=5m. The plane of motion of the particle is vertical and perpendicular to the walls. Assuming that all the collisions are perfectly elastic, find the maximum height attained by the particle and the total number of collisions suffered by the particle with the walls before it hits ground. Take g=10m/s2.

View SolutionA ladder 5m long rests against a vertical wall. If its top slides down at the rate of 10cm/sec, then, when the foot of the ladder is 4m away from the wall, the angle between the floor and the ladder is decreasing at the rate of
View SolutionA small ball is projected at an angle α with an initial velocity u between two vertical walls such that in the absence of the wall its range would have been 5d. Given that all the collisions are perfectly elastic and distance between the walls be d2, find.
(a) maximum height atained by the ball.
(b) total number of collisions with the walls before the ball comes back to the ground, and
(c) point at which the ball finally falls. The walls are supposed to be very tall.

View Solution
