A cylindrical tube of uniform cross-sectional area A is fitted with two air tight frictionless postion.
The pistons are connected to each other by a metallic wirte. Initially the pressure of the gas is $p_{o}$ and temperature is $T_{o},$ atmospheric pressure is also $p_{o}$ Now the temperature of the gas is increased to $2 T_{0},$ the tension in the wire will be

A

$2 p_{o} A$

B

$p_{o} A$

C

$\frac{p_{o} A}{2}$

D

$p_{o} A$

Text Solution

Verified by Experts

The correct Answer is:B

Volume of the gas is constant
V= constant

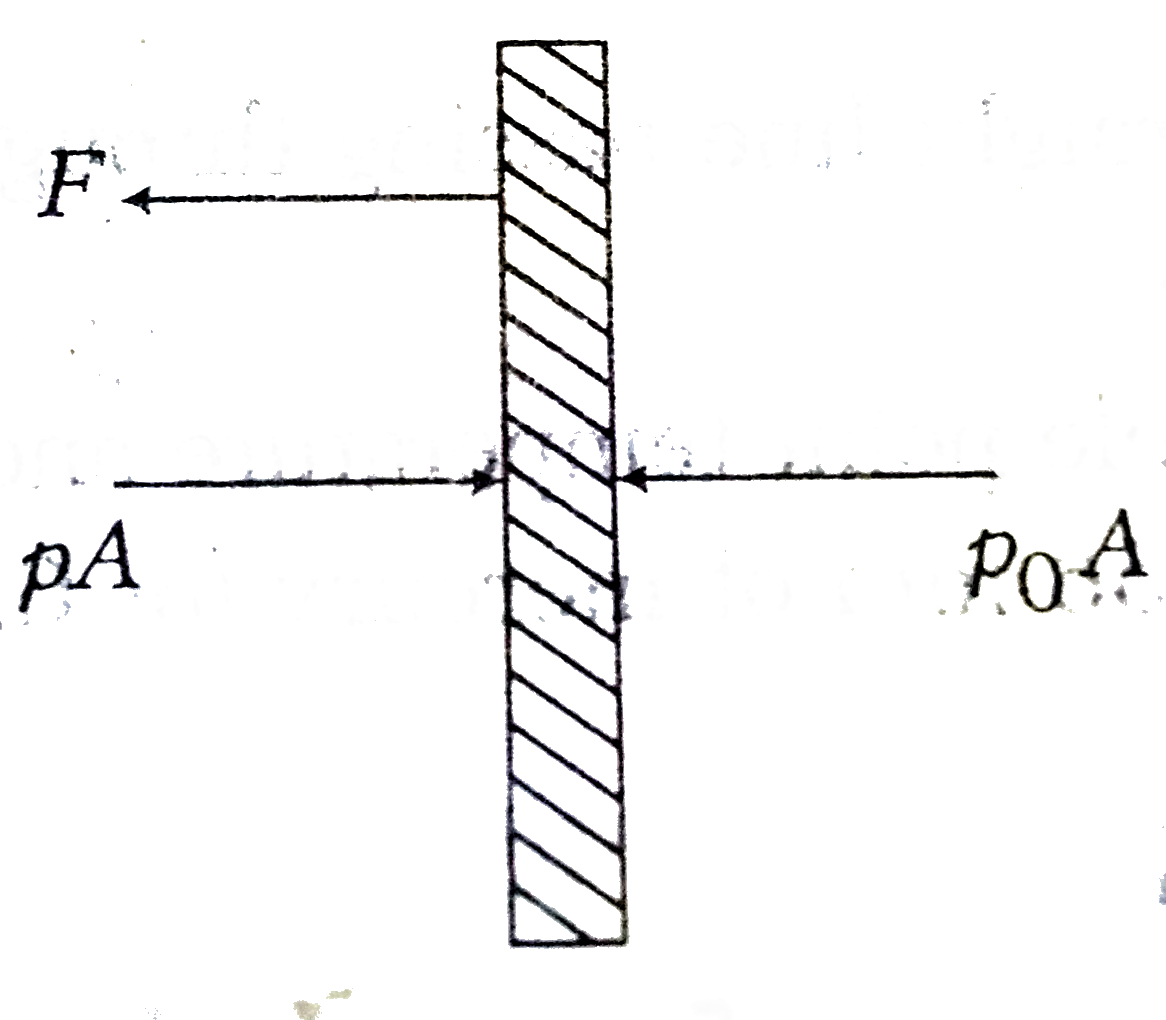
$∴ \propto T i . e .,$ Pressure will be doubled, temperature is doubled
$∴ p = 2 p_{o}$
Now let F be the tension in the wire. Then equilibrium of any one piston gives.
$F = (p - p_{o}) A = (2 p_{o} - p_{o}) A = p_{o} A$

|

Updated on:21/07/2023

Class 11 PHYSICS THERMAL EXPANSION AND CALORIMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

A cylindrical tube of uniform cross-sectional area A is fitted with two air tight frictionless pistons. The pistons are connected to each other by a metallic wire. Initially the pressure of the gas is $P_{0}$ and temperature is $T_{0}$ , atmospheric pressure is also $P_{0}$ . Now the temperature of the gas is increased to $2 T_{0}$ , the tension in the wire will be
A $2 P_{0} A$
B $P_{0} A$
C $\frac{P_{0} A}{2}$
D $4 P_{0} A$
Question 2 - Select One
Two identical containers joned by a small pipe initially contain the same gas at pressue $p_{o}$ and abosolute temperature $T_{o^{.}}^{.}$ One container is now mantained at the same temperature while the other is heated to $2 T_{0^{.}}^{.}$ The commmon pressure of the gases will be
A $\frac{3}{2} p_{o}$
B $\frac{4}{3} p_{o}$
C $\frac{3}{5} p_{o}$
D $2 p_{o}$
Question 3 - Select One
Two idential container joined by a small pipe initially contain the same gas at pressure $p_{0}$ and absolute temperature $T_{0}$ . One container is now maintained at the same temperature while the other is heated to $2 T_{0}$ . The common pressure of the gas
A $\frac{3}{2} p_{0}$
B $\frac{4}{3} p_{0}$
C $\frac{5}{p_{0}}$
D $2 p_{0}$

DC PANDEY-THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES-A Tacking it together

Home
Ask Doubt
Profile