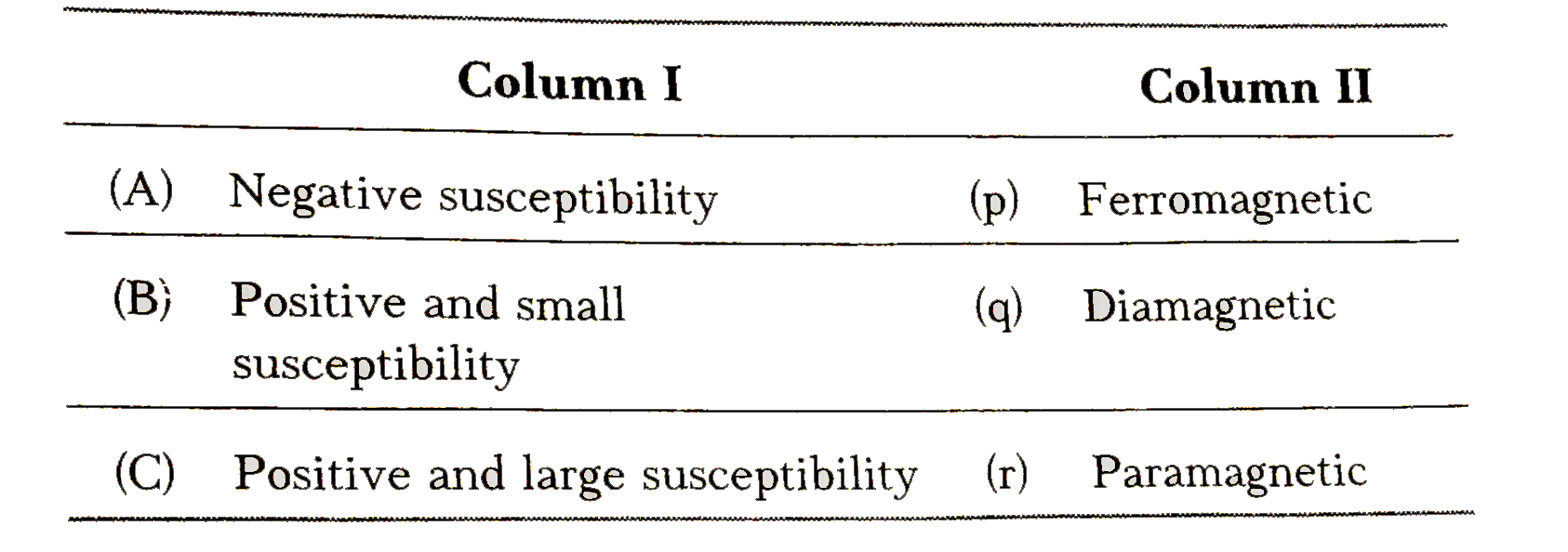Consider the expression for magnetic potential energy Um obtained in previous question, match the tems of colum I with the tems of Column II and choose the correct option from the codes given below.
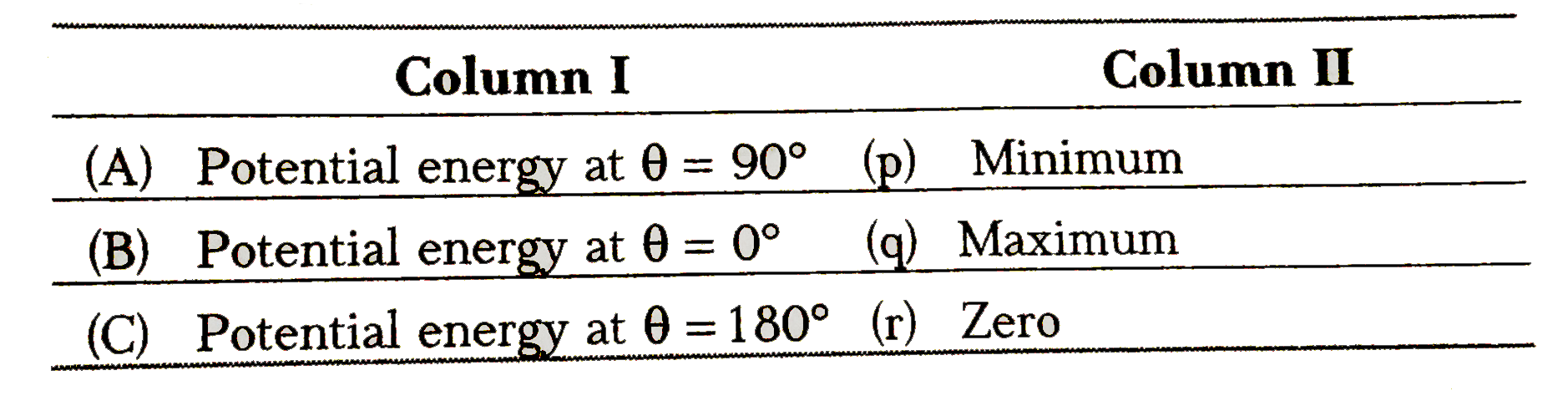
Video Solution
Text Solution
The correct Answer is:A-R,B-P,C-Q
Since the magnetic potential energy Um is given by.
Um=m.B=−mBcosθ
A Forθ=90∘⇒Um=−mBcos90∘=0
B Forθ=0∘,Um=−mBcos0∘=−mB
The potential energy is minimum and hence the middle the needle is in most stable position.
C Forθ=180∘,Um=−mBcos180∘=+mB
|
Similar Questions
Knowledge Check
Match the items of column I with the items of column II and choose the correct option from the codes given below.
 A
A B
B C
C D
D
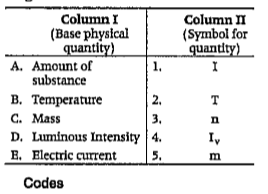
Match the terms of column I with the items of column II and choose the correct option from the codes given below.
 A
A B
B C
C D
D
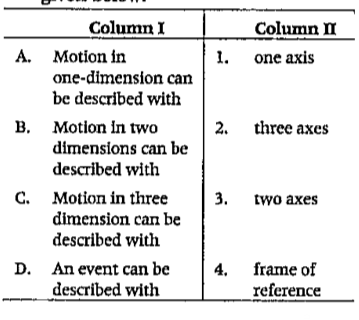
Match the terms of Column I with the items of Column II and choose the correct options from the codes given below.
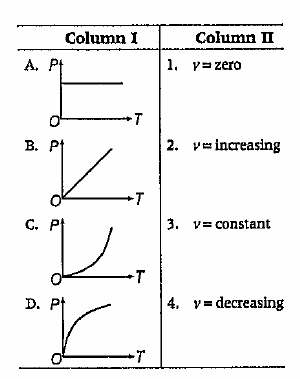 A
A B
B C
C D
D
Match the terms of Column I with the items of Column II and choose the correct option from the codes given below.
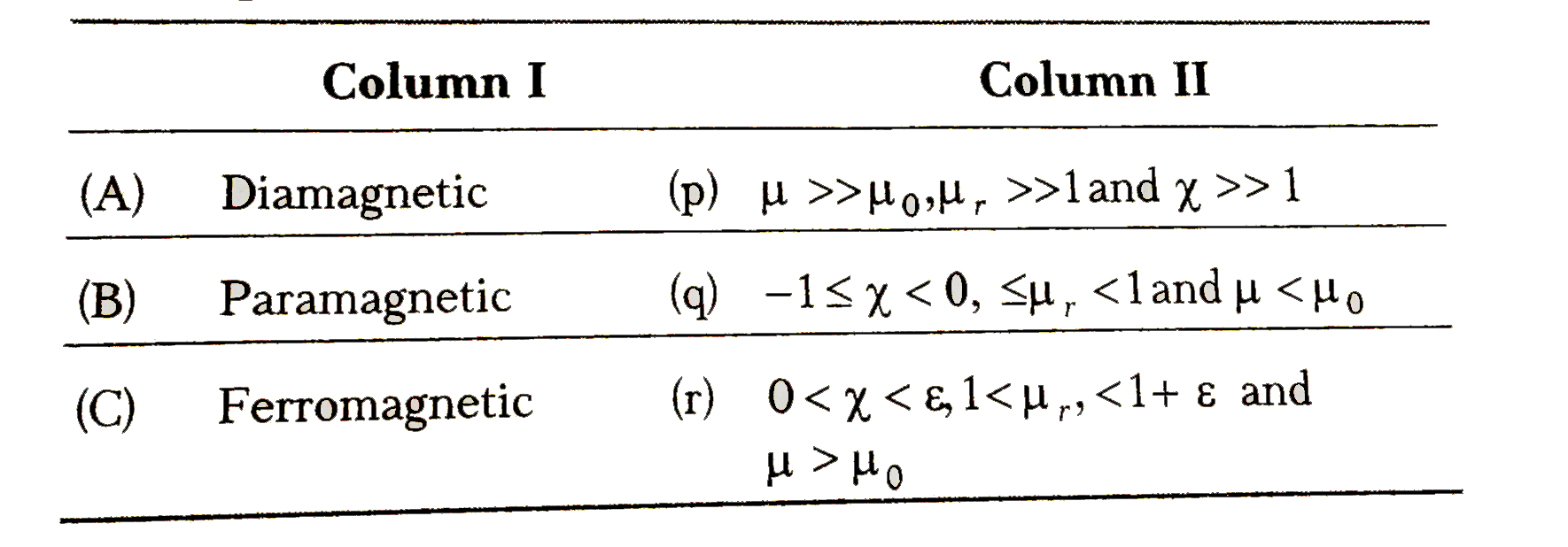
View SolutionMatch the terms of Column I with those of Column II and choose the correct option from the codes given below.
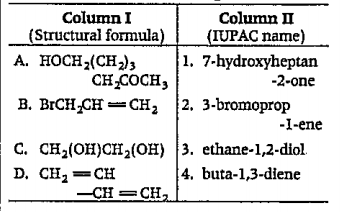
View SolutionMatch the terms of Column I with those of Column II and choose the correct option from the codes given below.
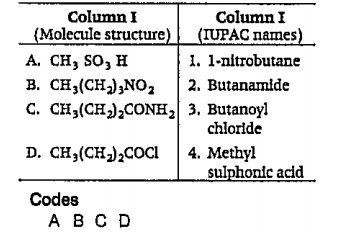
View SolutionMatch the items of Column I with items of Column II and choose the correct option from the codes given below:

View SolutionMatch the terms of Column I with the terms of the Column II and choose the correct option from the codes given below.
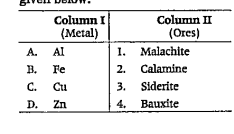
View Solution