Assertion A magnetic is dropped along the axis of a circular conducting loop as shown in figure. Then, acceleration of magnet is always less than g.
Reason when magnet is above the loop, then it will repel the magnet and when it is below the loop, then it will attract the magnet.
Reason When magnet is above the loop, then it will repel the magnet and when it is below the loop, then it will attract the magnet.

If both Assertion and Reason are corrent and Reason is the corrent explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is ture.
The correct Answer is:A
This is in accordance with Lenz's law. When magnet is above the loop, then north pole is formed and hence will repel and when it is below the loop, then it will attract the magnet.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Knowledge Check
The magnetic field at the centre of circular loop in the circuit shown below is
 Aμ04π2Ir(1+π)Bμ04π2Ir(π−1)Cμ04π2IrDμ04πIr(π+1)
Aμ04π2Ir(1+π)Bμ04π2Ir(π−1)Cμ04π2IrDμ04πIr(π+1)The magnetic field at the centre of circular loop in the circuit shown below is
 Aμ04π2Ir(1+π)Bμ04π2Ir(π−1)Cμ04π2IrDμ04πIr(π+1)
Aμ04π2Ir(1+π)Bμ04π2Ir(π−1)Cμ04π2IrDμ04πIr(π+1)The magnetic field at the centre of the circular loop as shown in Fig. when a single wire is bent to form a circular loop and also extends to form straight sections is
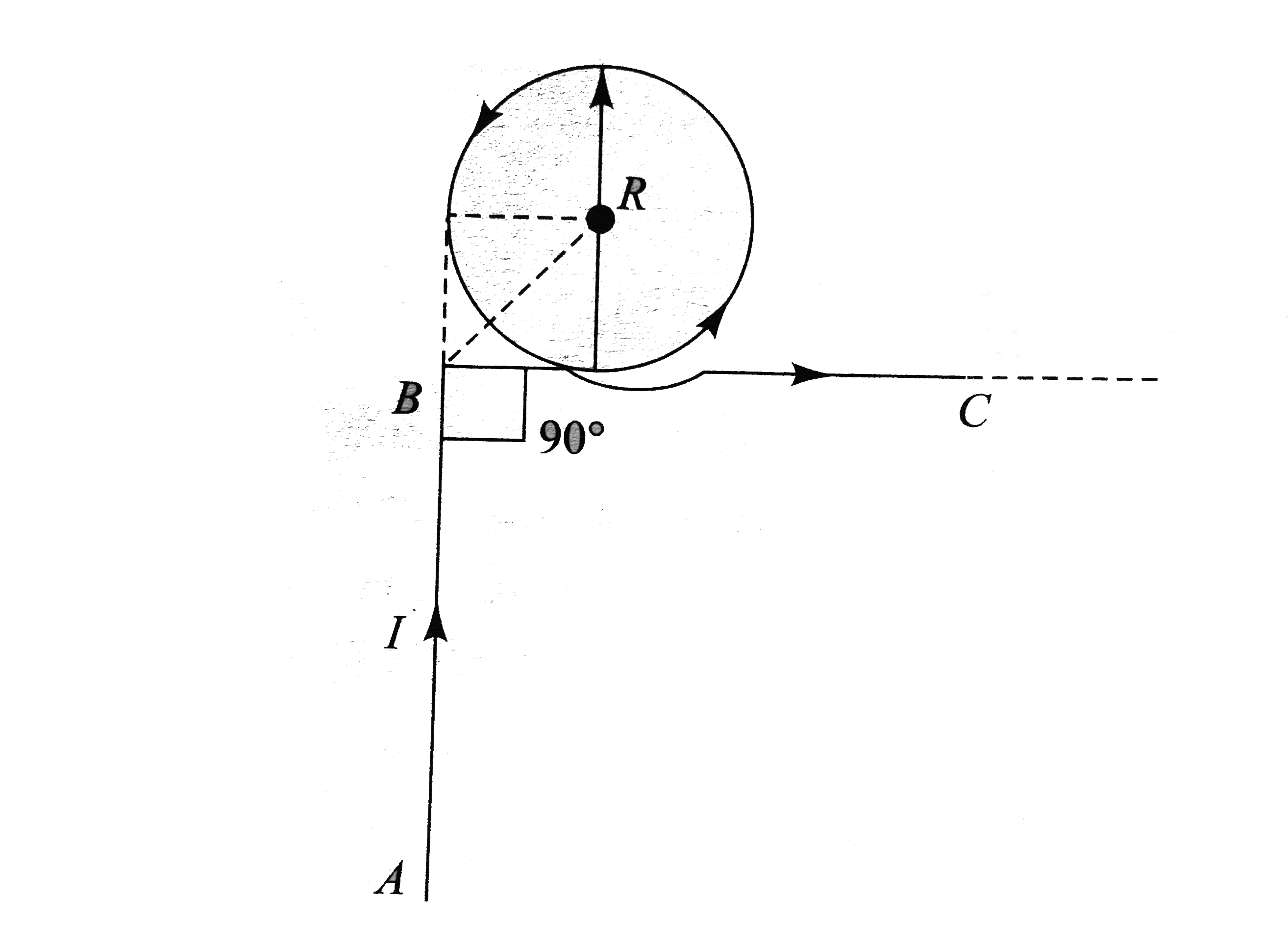 Aμ0I2R⊙Bμ0I2R(1+1π√2)⊙Cμ0I2R(1−1π√2)⊗Dμ0IR(1−1π√2)⊗
Aμ0I2R⊙Bμ0I2R(1+1π√2)⊙Cμ0I2R(1−1π√2)⊗Dμ0IR(1−1π√2)⊗
Find the magnetic field at the centre of the circular loop shown in figure.

View SolutionThe magnetic field at the centre of the circular loop as shown in Fig. when a single wire is bent to form a circular loop and also extends to form straight sections is
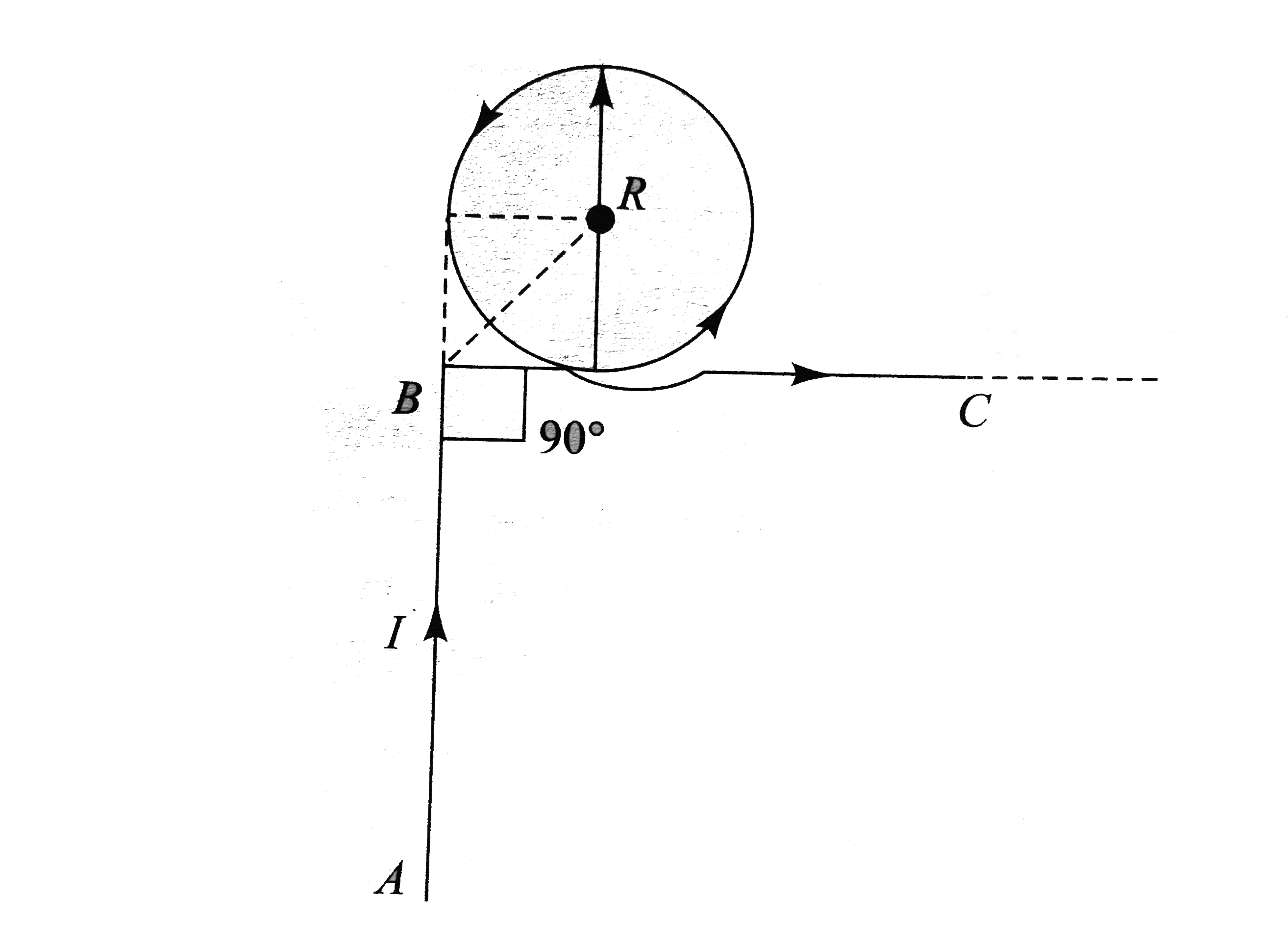
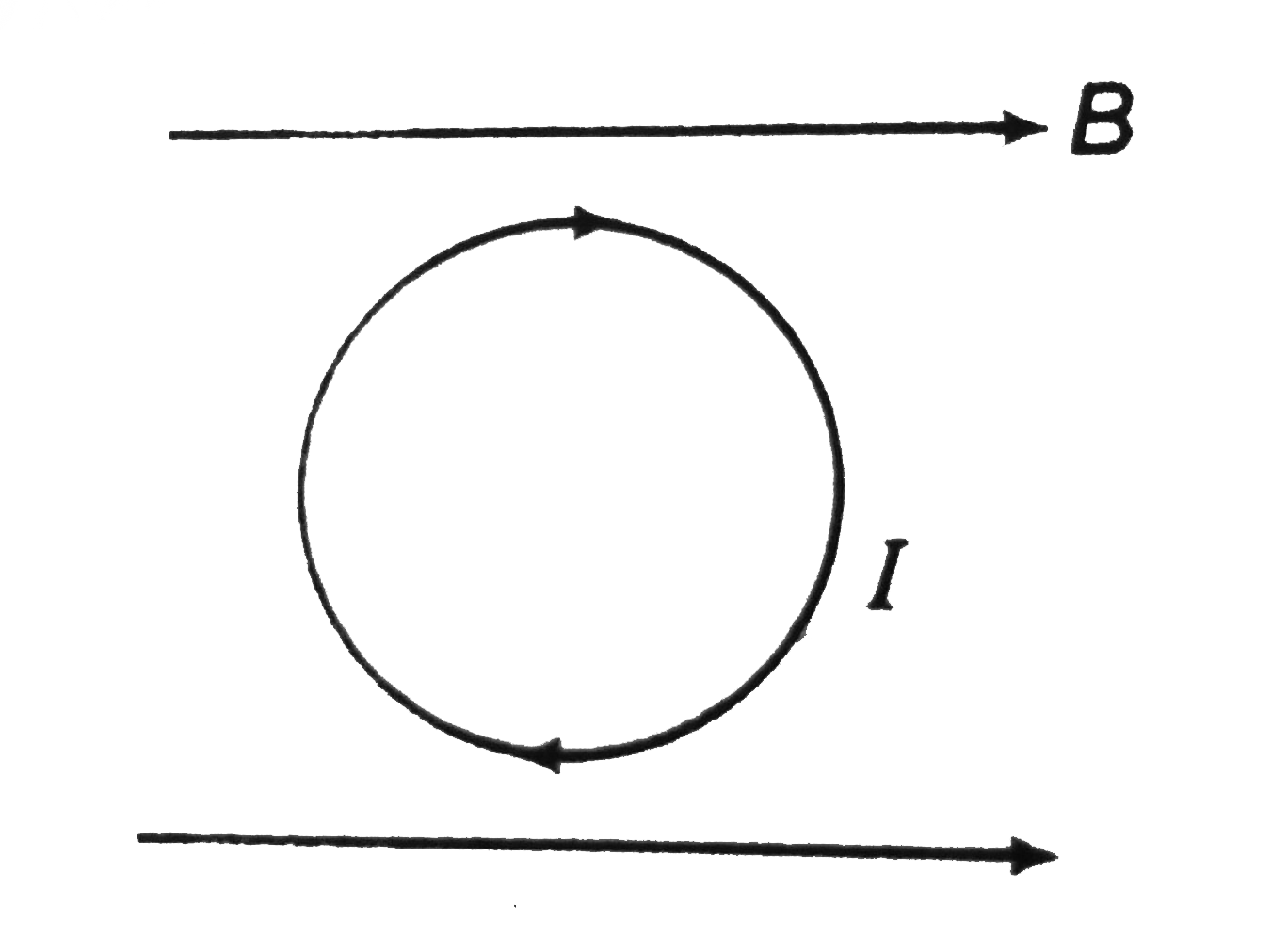
View SolutionAssertion : A current carrying loop is placed in uniform magnetic field as shown in figure. Torque in the loop in this case is zero.
Reason : Magnetic moment vector of the loop is perpendicular to paper inwards.
View SolutionA current loop in a magnetic field
View SolutionAssertion : A current carrying loop is placed in uniform magnetic field as shown in figure. Torque in the loop in this case is zero.
Reason : Magnetic moment vector of the loop is perpendicular to paper inwards.

View Solution

