Assertion Coefficient of self-induction of an inductor depends upon the rate of change of current passing through it.
Reason From, e=−Ldidt
We can see that, L=−e(di/dt)orL∝1(di/dt)
If both Assertion and Reason are corrent and Reason is the corrent explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is ture.
The correct Answer is:D
Self-inductance does not depend upon current flowing or change in current flowing but it depends upon turns N. Area of cross-section (A) and permeabillity of medius (μ).
We have, =didt.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Match the columns
Explore 5 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Medical entrances gallery
Explore 25 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Taking it together
Explore 119 Videos
- CURRENT ELECTRICITYBook:DC PANDEYChapter:CURRENT ELECTRICITYExercise:Medical entrances gallery
Explore 97 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEYChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
Similar Questions
Self induction is the property of a coil by virture of which the coil oppose any change in the strenght of current flowing through it by inducting an e.m.f. in itself.
Self induction represents electric inertia which is measured in terms of coefficient of self inductance
We can show that L=ϕI=−edI/dt
Read the above passage and answer the following questions :
An e.m.f. of 150 microvolt is induced in a coil when current in it changes from 5A ot 1 A in 0.2 sec. what is self inductance of the coil ?
(ii) How does self indcution of a coil represent its electric inertia ?
(iii) What is them implication of this property in our daily life ?
View SolutionIn an inductor of self-inductance L=2 mH, current changes with time according to relation i=t2e−t. At what time emf is zero ?
View Solution
Knowledge Check
Assertion : There can be induced e.m.f. in an inductor even if the current through it is zero.
Reason : Induced e.m.f. depends upon the rate of change of current rather than the current itself.AAssertion is true and Reason is correct explanation of AssertionBAssertion is true and Reason is falseCAssertion and Reason both are falseDAssertion is false but Reason is trueThe coefficients of self induction of two coils are L1 and L2 .To induce an of 2 volt in the coil, a change of current of 1A has to be produced in 5 second and 50ms respectively. The ratio of their self inductances L1:L2 will be
A1:5B200:1C100:1D50:1Assertion : Angular frequency of LC oscillations is 2rad/s and maximum current in the circuit is 1A. Then, maximum rate of change of current should be 2A/s.
Reason: (dIdt)max=(Imax)ωAIf both Assertion and Reason are true and the Reason is correct explanation of the Assertion.BIf both Assertion and Reason are true but Reason is not the correct explanation of AssertionCIf Assertion is true, but the Reason is false.DIf Assertion is false but the Reason is true.
As per phenomenon of electromagnetic induction an emf is induced in a coil when a magnetic flux linked with it changes. It is possible that emf is induced in single isolated coil due to change of magnetic flux through the coil by means of varying the current passing through the same coil. This phenomenon is called 'self-induction'. If we have coil of N turns closely wound together and a current I is passed through the coil then total magnetic flux associated with it
NϕB∝IorNϕB=LI ...... (1)
Here ϕB = flux linked with each turn of a coil. The proportionality constant L is known the self-inductance of the coil and its value depends on the dimensions of the coil and nature of core material. If the current flowing through the coil changes then an induced emfe is set up as :
ɛ=−ddt(NϕB)=−LdIdt ......(ii)
(a) Define self-inductance of a coil in terms of induced emf.
(b) Obtain SI unit of self inductance.
(c) Write its dimensions.
(d) Do you agree with the statement "Self-inductance is electromagnetic analogue of mass in mechanics" ?
(e) Why do we see some spark in the switch of an electric fan when a running fan is switched off?
View SolutionThe current through two inductors of self inductance 12 mH and 30 mH is increasing with time at the same rate. Draw graphs showing the variation of the (a ) e.m.f. induced with the rate of change of current in each inductor. (b) enargy stored in each inductor with the current flowing through it.
Compare the energy stored in the coils if power dissipated in the coil is same.
View SolutionAssertion : When number of turns in a coil is doubled, coefficient of self-inductance of the coil becomes 4 times.
Reason : This is because L∝N2
View SolutionA capacitor can be used to produce a desired electric field. We consldered the parallel plate arrangement as a basic type of capacitor. Similarly, an inductor (symbol ) con be used to near the middle of a long solenoid ) as our basic type fo inductor.
if we establish a current i in the winding ( or turns ) of an inductro ( a solenoid ) the current produces a magnetic flux ϕB through the central region of the inductor. the inductance of the inductor is then
[L=NϕEi] ( inductance defined )
where N is the number of turns. the windings of the inductor are said to the linked by the shared flux, and the product NϕE is called the magnetic flux linkage . the inductance L is thus a measure of flux produced by the inductor per unit of current . Now, consider a special type of inductor whose radius of turn R as shown in the adjacent figure and total number of turns is N.
This special type of solenoid produces a magnetic field ∣∣→B∣∣=μlr2 uniformly along the axis of the solenoid as shown in figure. r is the distance from the axis of solenoid.

The value of total flux linkages when current l flows through this special type of inductor is given by
View SolutionA capacitor can be used to produce a desired electric field. We consldered the parallel plate arrangement as a basic type of capacitor. Similarly, an inductor (symbol ) con be used to near the middle of a long solenoid ) as our basic type fo inductor.
if we establish a current i in the winding ( or turns ) of an inductro ( a solenoid ) the current produces a magnetic flux ϕB through the central region of the inductor. the inductance of the inductor is then
[L=NϕEi] ( inductance defined )
where N is the number of turns. the windings of the inductor are said to the linked by the shared flux, and the product NϕE is called the magnetic flux linkage . the inductance L is thus a measure of flux produced by the inductor per unit of current . Now, consider a special type of inductor whose radius of turn R as shown in the adjacent figure and total number of turns is N.
This special type of solenoid produces a magnetic field ∣∣→B∣∣=μlr2 uniformly along the axis of the solenoid as shown in figure. r is the distance from the axis of solenoid.
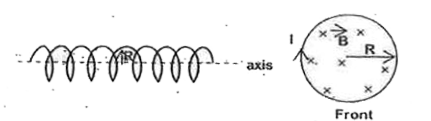
Value of self inductance of this inductor is given by
View Solution