A circuits contains a capacitor and inductance each with negligible resistance. The capacitor is initially charged and the charging battery is disconnected. At subsequent time , the charge on the capacitor will
increase exponentially
decrease exponentially
decrease linearly
remain constant
The correct Answer is:C
Similar Questions
Knowledge Check
A parallel plate capacitor is charged and then the battery is disconnected. When the plates of the capacitor are brought closer, then
Aenergy stored in the capacitor decreasesBthe potential differences between the plates decreasesCthe capacitance increasesDthe electric field between the plates decreasesAn uncharged capacitor is connected to a battery. On charging the capacitor
AAll the energy supplied is stored in the capacitorBHalf the energy supplied is stored in the capacitorCThe energy stored depends upon the capacity of the capacitor onlyDThe energy stored depends upon the time for which the capacitor is chargedA parallel plate capacitor is charged and the charging battery is then disconnected. If the plates of the capacitor are moved farther apart by means of insulating handles:
A(a) the charge on the capacitor increases.B(b) the voltage across the plates increases.C(c) the capacitance increases.D(d) the electrostatic energy stored in the capacitor increases
Three initially uncharged capacitors are arranged with batteries as shown in. Find the charge on each capacitor.
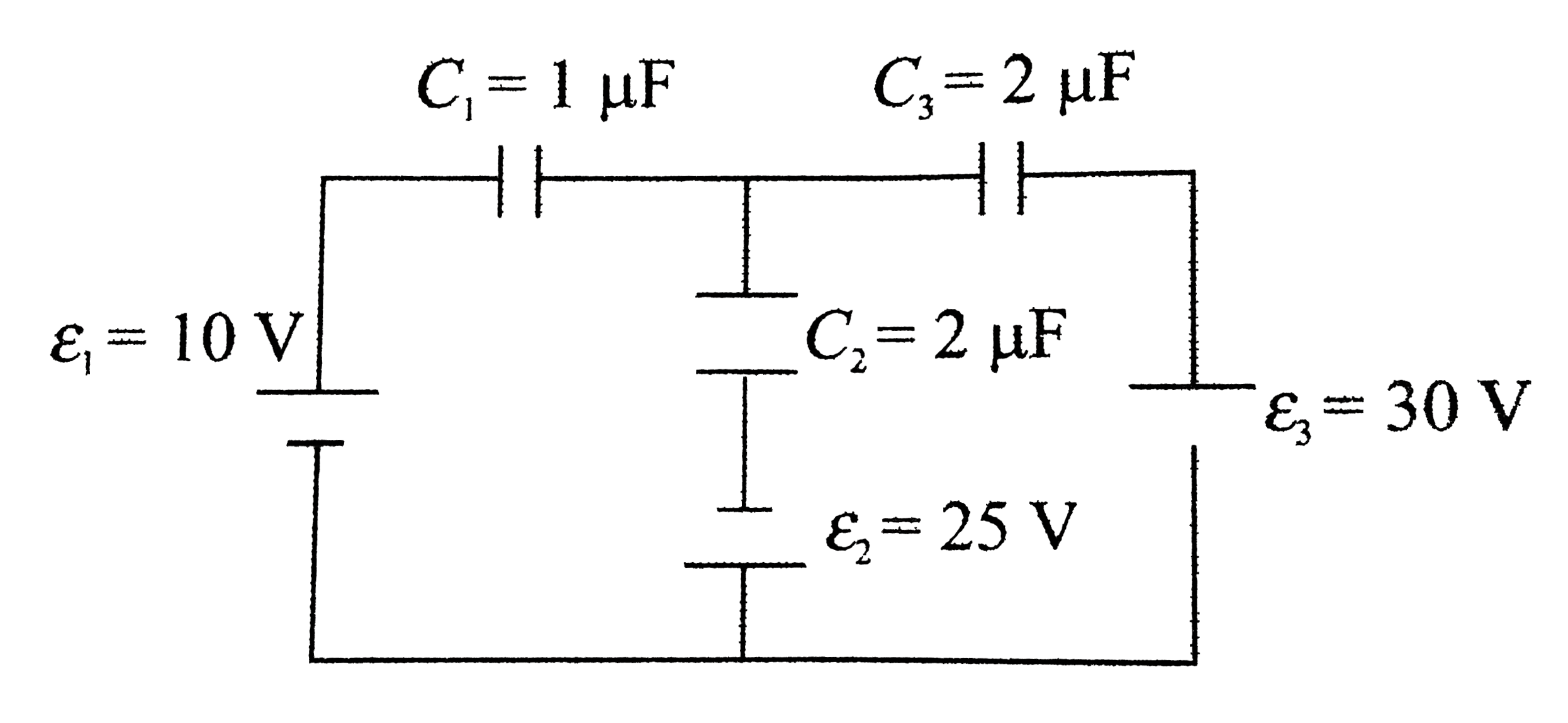 .
.
View SolutionA parallel plate capacitor is charged and the charging battery is then disconnected. If the plates of the capacitor are moved farther apart by means of insulating handles:
View SolutionSolve Problem 25.1 assuming the capacitor to have been initially charged and subsequently disconnected before the mica sheet is inserted in it.
View SolutionSolve Problem 25.1 assuming the capacitor to have been initially charged and subsequently disconnected before the mica sheet is inserted in it.
View SolutionIn the fig. shown the circuit is in steady state.
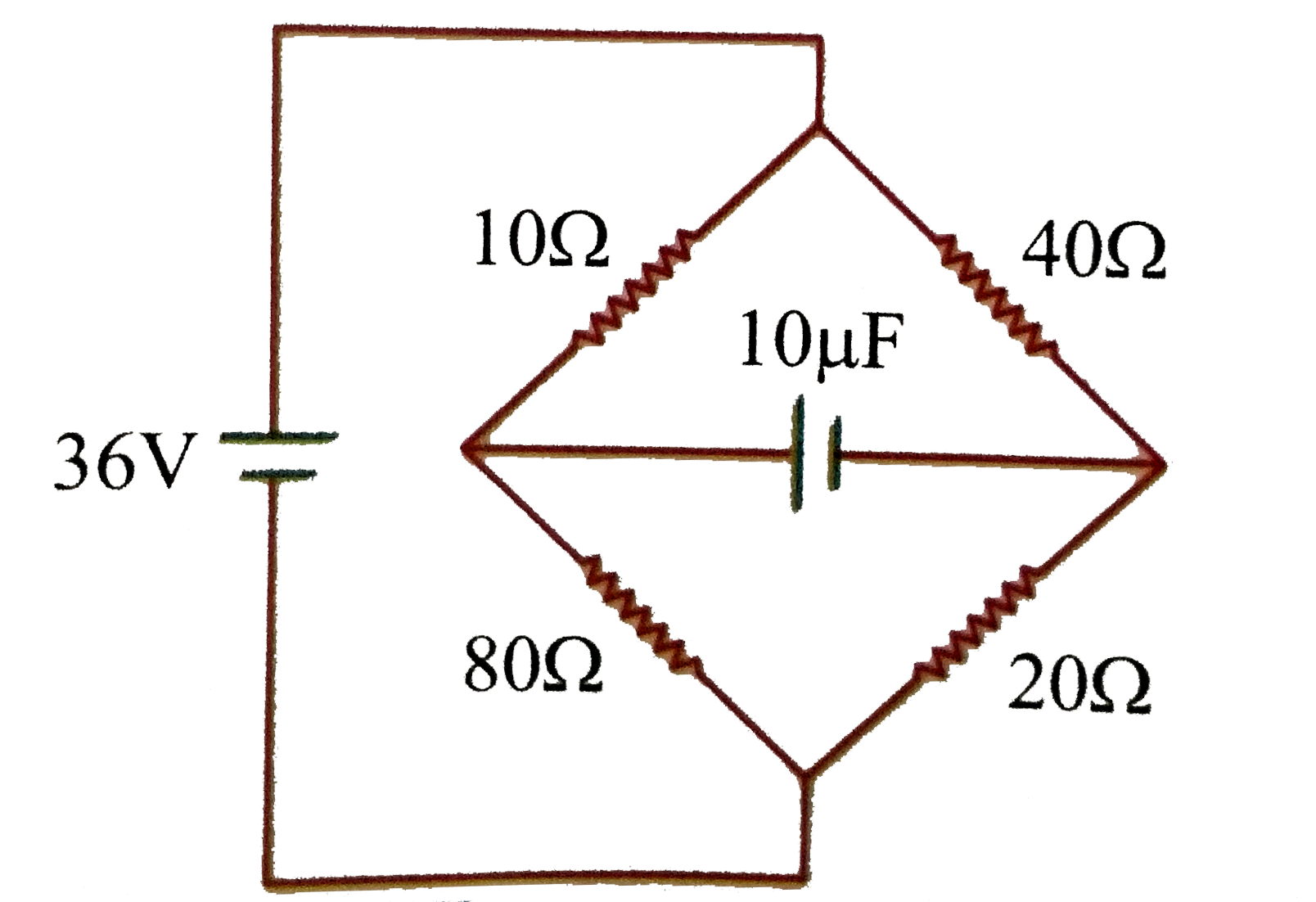
If the battery is disconnected give the capacitor charge as a function of time.
View Solution
