The wavelength of th first spectral line of sodium 5896 Å . The fisrt excitation potential of sodium atomm will be (Planck's constant h=6.63×10−34J−s)
4.2V
3.5V
2.1V
None of these
The correct Answer is:C
To find the first excitation potential of a sodium atom given the wavelength of its first spectral line, we can use the relationship between energy and wavelength. The energy of a photon can be calculated using the formula:
E=hcλ
Where:
- E is the energy of the photon,
- h is Planck's constant (6.63×10−34J s),
- c is the speed of light (3.00×108m/s),
- λ is the wavelength in meters.
Step 1: Convert Wavelength to Meters
The given wavelength is 5896Å (angstroms). We need to convert this to meters:
λ=5896Å=5896×10−10m
Step 2: Use the Energy Formula
Now, substitute the values into the energy formula:
E=(6.63×10−34J s)(3.00×108m/s)5896×10−10m
Step 3: Calculate the Energy
Now, perform the calculation:
1. Calculate the numerator:
6.63×10−34×3.00×108=1.989×10−25J m
2. Calculate the energy:
E=1.989×10−255896×10−10=1.989×10−255.896×10−7≈3.375×10−19J
Step 4: Convert Energy to Electron Volts
To convert joules to electron volts, use the conversion factor 1eV=1.6×10−19J:
E≈3.375×10−19J1.6×10−19J/eV≈2.11eV
Conclusion
The first excitation potential of the sodium atom is approximately 2.11eV.
---
- E is the energy of the photon,
- h is Planck's constant (6.63×10−34J s),
- c is the speed of light (3.00×108m/s),
- λ is the wavelength in meters.
The given wavelength is 5896Å (angstroms). We need to convert this to meters:
Now, substitute the values into the energy formula:
Now, perform the calculation:
6.63×10−34×3.00×108=1.989×10−25J m
E=1.989×10−255896×10−10=1.989×10−255.896×10−7≈3.375×10−19J
To convert joules to electron volts, use the conversion factor 1eV=1.6×10−19J:
The first excitation potential of the sodium atom is approximately 2.11eV.
Topper's Solved these Questions
- ATOMSBOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - ASSERTION AND REASON
10 Videos
- ATOMSBOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - MATCH THE COLUMNS
4 Videos
- ATOMSBOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - Check point 12.3
15 Videos
- ALTERNATING CURRENTBOOK - DC PANDEYCHAPTER - ALTERNATING CURRENTEXERCISE - JEE MAIN
63 Videos
- CAPACITORSBOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
Similar Questions
Give the order of the following :
Planck's constant (6.63×10−34J-s)
View SolutionThe stopping potential V0 (in volt) as a function of frequency (v) for a sodium emitter, is shown in the figure. The work function of sodium, from the data plotted in the figure, will be:
(Given : Planck’s constant)
(h)=6.63×10−34Js electron charge e=1.6×10−19C)
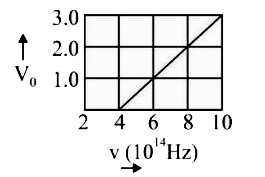
View Solution
Knowledge Check
The wavelength of yellow line of sodium is 5896Å. Its wave number will be
A50883×1010 per secondB16961 per cmC17581 per cmD50883 per cmThe momentum of a photon of de Broglie wavelength 5000Å is …………… .
[Plank's constant =6.63×10−34J.s]A1.326×10−28kg−m/sB7.54×10−28kg−m/sC1.326×10−27kg−m/sD7.54×10−27kg−m/sA 160 watt light source is radiating light of wavelength 6200 Å uniformly in all directions. The photon flux at a distance of 1.8 m is of the order of (Planck's constant 6.63×10−34J−s)
A102m−2s−1B1012m−2s−1C1019m−2s−1D1025m−2s−1
Hydrogen atom in its ground state is excited by means of monochromatic radiation of wavelength 970.6Å. How many lines are possible in the resulting emission spectrum ? Calculate the longest wavelength amongst them. You may assume that the ionisation energy for hydrogen atom is 13.6 eV. Given Planck's constant =6.6×10−34Js, c=3×10(8)ms−1
View SolutionCalculate the de Broglie wavelength of an electron moving with 1/3rd of the speed of light in vacuum.
(Neglect relativistic effect)
(Planck's constant : h=6.63×10−34Js, Mass of electron : m=9.11×10−28g)
View SolutionThe work function of a metal is 1.6×10−19J. When the metal surface is illuminated by the light of wavelength 6400Å, then the maximum kinetic energy of emitted photo - electrons will be
(Planck's constant h=6.4×10−34Js)
View SolutionWhen an electron in hydrogen atom is excited, from its 4th to 5the stationary orbit, the change in angular momentum of electron is (Planck's constant: h=6.6×10−34J−s)
View SolutionA 160 watt light source is radiating light of wavelength 6200Å uniformly in all directions. The photon flux at a distance of 1.8m is of the order of (Plank's constant 6.62×10−34J−s)
View Solution
