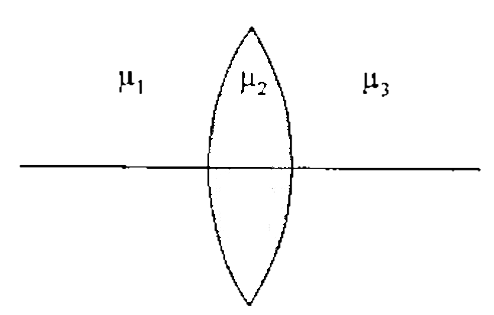
A thin symmettrical double convex lens of refractive index μ2−1.5 is placed between a medium of refractiv eindex μ1=1.4 to the left and another medium of refractive index μ3=1.6 to the right.Then the system behaves as
a convex lens
a concave lens
a glass plate
a convexo concave lens
The correct Answer is:C
For first refraction surface.
For parallel beam of light, −μ1u+μ2V=μ2−1R
⇒−1.40∞+1.5V=1.5−1.4R⇒V=15R
For second refraction surface,
−μ21.5r+μ3V=μ2®
⇒−1.515R+1.6V=1.6−1.5R⇒V'=∞
Hence ,the combination behaves as glass plate
Topper's Solved these Questions
Similar Questions
Knowledge Check
If a convex lens of refractive index μl is placed in a medium of refractive index μm Such that μl>μm>μair then
AThe nature of the lens is divergingBThe nature of the lens is convergingCThe nalure of the lens may be converging or divergingDThe nature of the lens can't be determinedA lens made of material of Refractive index μ2 is surrounded by a medium of Refractive Index μ1. The focal length f is related as
Af∝(μ2−μ1)Bf∝μ1(μ2−μ1)Cf∝(μ2+μ1)Df∝1(μ2+μ1)A double convex lens of glass of refraction index μ is immersed in a medium of refractive index μ1. If a parallel beam emerges undeviated through the lens, then
Aμ=μ1Bμ=1μ1Cμ>μ1Dμ<μ1
A lens made of material of Refractive index μ2 is surrounded by a medium of Refractive Index μ1. The focal length f is related as
View SolutionA lens made of material of Refractive index μ2 is surrounded by a medium of Refractive Index μ1. The focal length f is related as
View SolutionA convex lens of refractive index μg is held in a reansparent medium of refractive index μm If course of rays is as shown in Fig., how are μgandμm related ?
 .
.
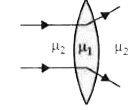
View SolutionA convex lens made up of material of refractive index μ1, is immersed in a medium of refractive index μ2 as shown in the figure. The relation between μ1 and μ2 is
View SolutionAn e.m. wave is travelling through a medium of refractive index μ1, and is incident on the boundary of a medium of refractive index μ2. IF the wave reflects at the boundary
View Solution