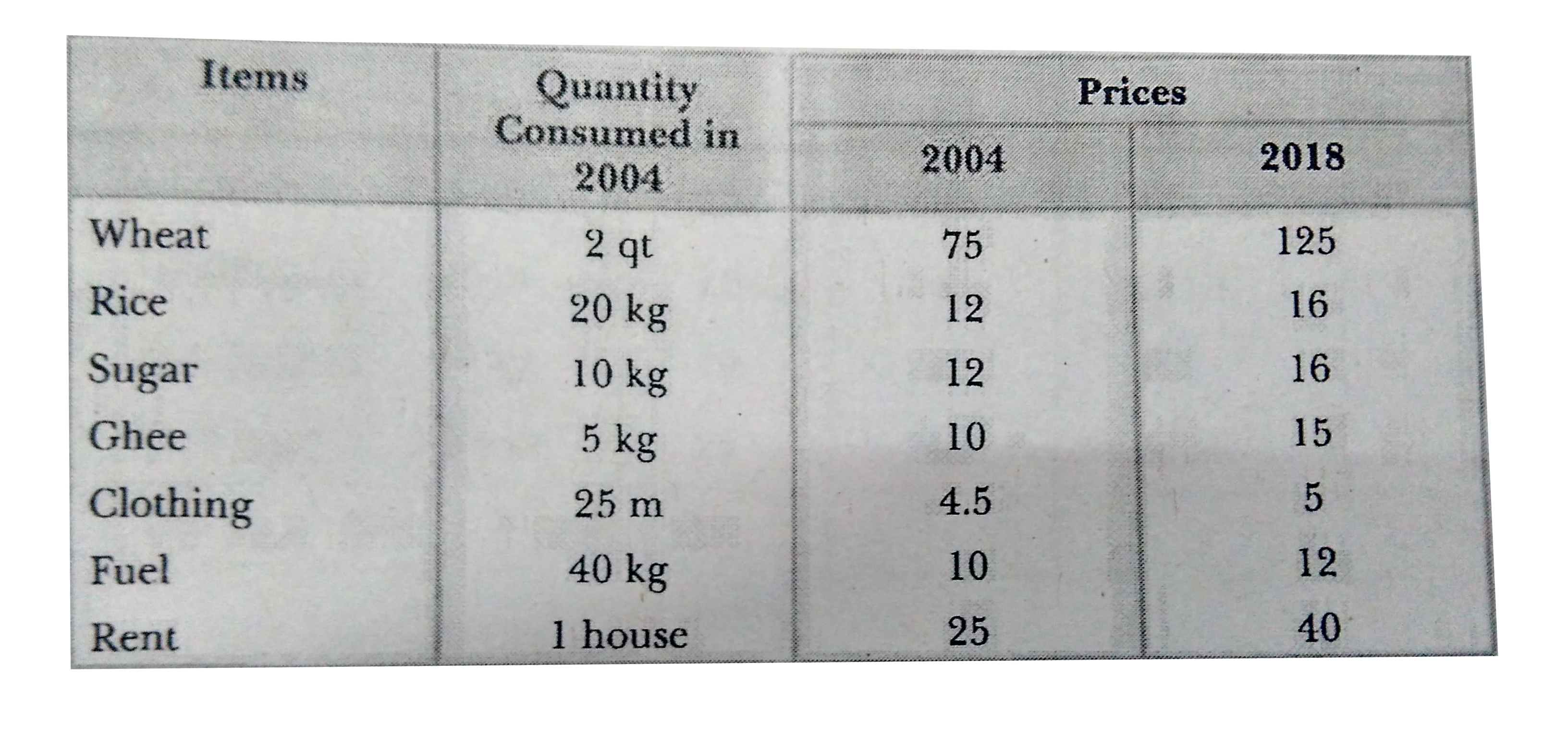
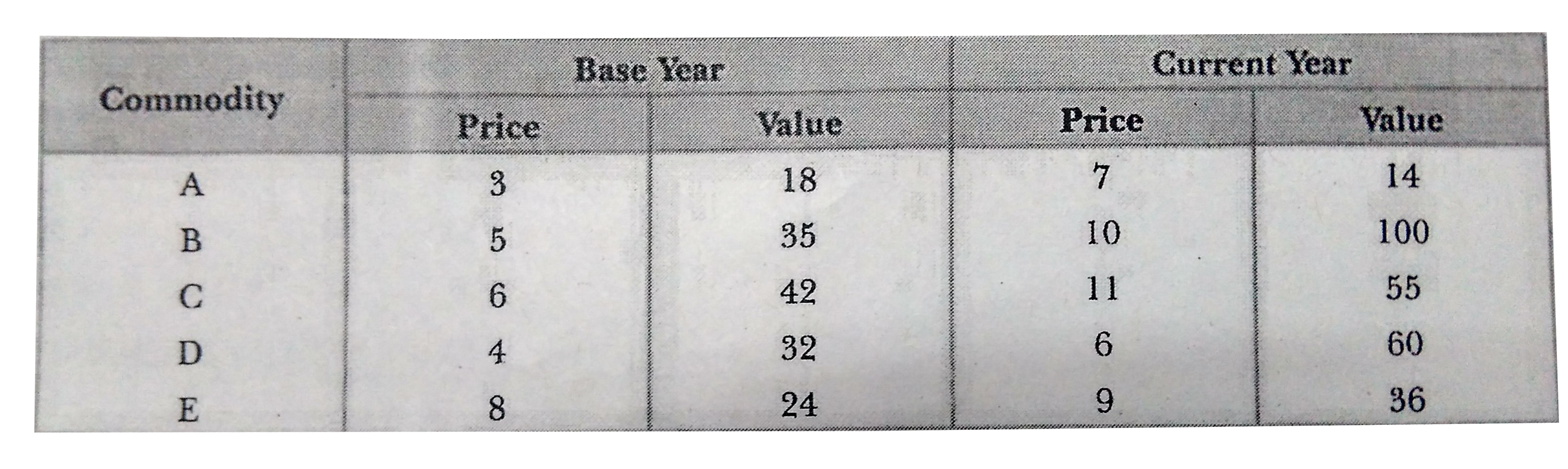
From the following data, find Fisher's Ideal Index Number:
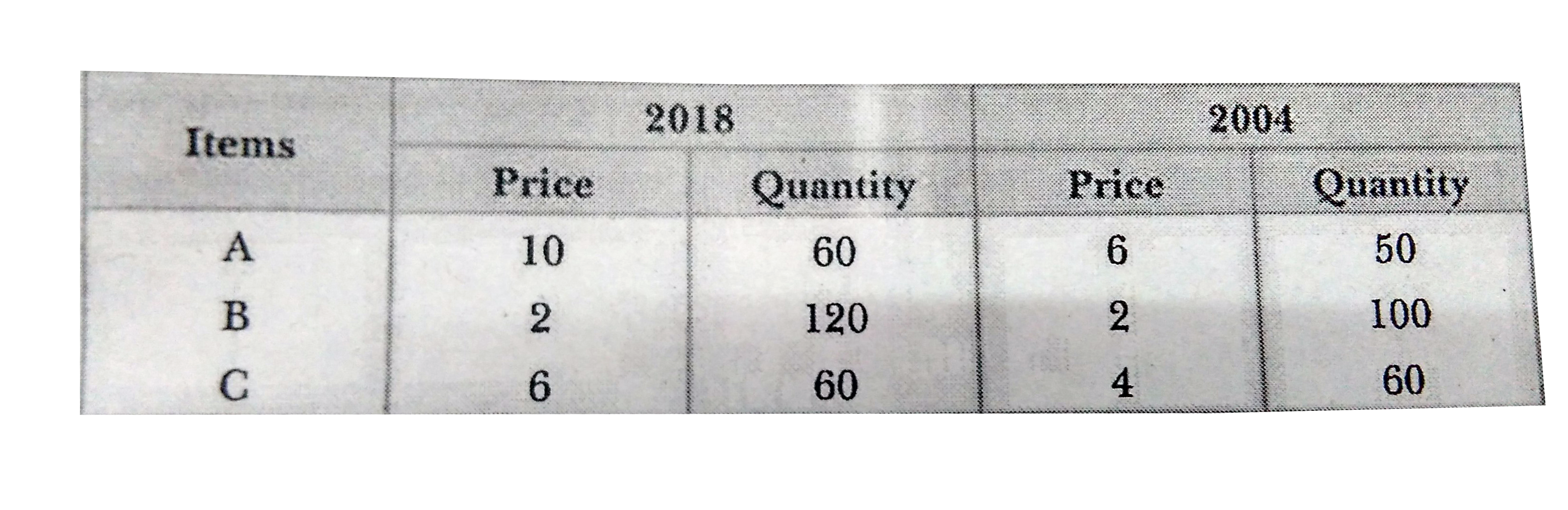
Video Solution
Text Solution
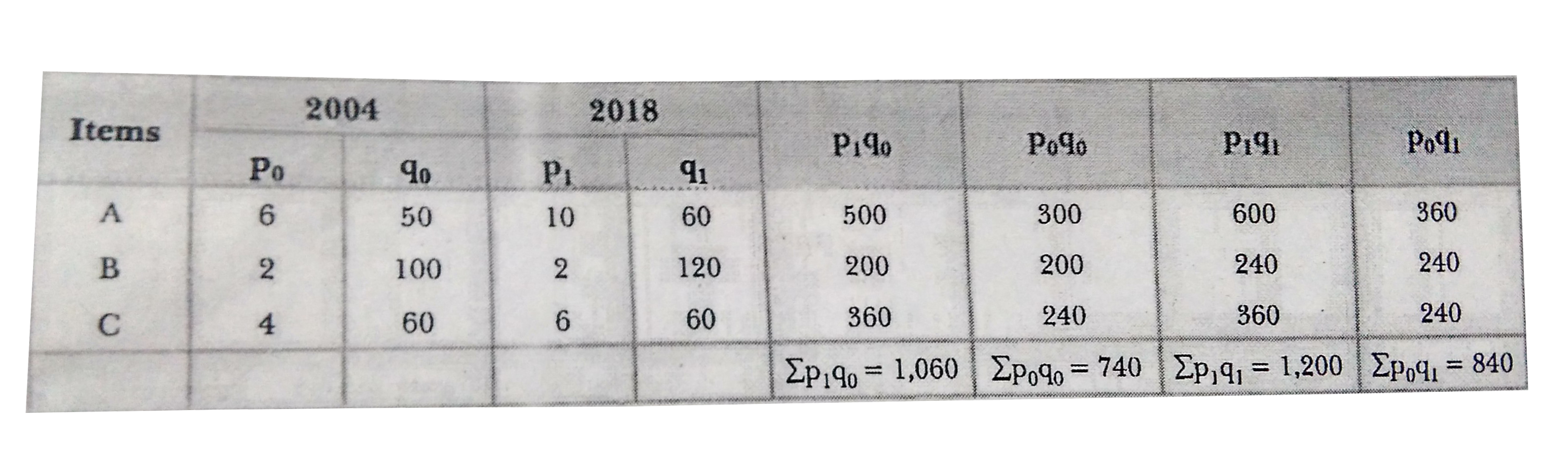
Fisher's Ideal Index Number
P01=√Σp1q0Σp0q0×Σp1q1Σp0q1×100
=√1,060740×1,200840×100
=√2.0463×100
=1.4305×100
= 143.05
|
Topper's Solved these Questions
- INDEX NUMBERSBOOK - TARUN JAIN & VK OHRICHAPTER - INDEX NUMBERSEXERCISE - A. Multiple Choice Questions: Choose the Correct Answer
12 Videos
- INDEX NUMBERSBOOK - TARUN JAIN & VK OHRICHAPTER - INDEX NUMBERSEXERCISE - B. Choose appropriate word and fill in the blank
7 Videos
- FREQUENCY DIAGRAMS - HISTOGRAM, POLYGON AND OGIVEBOOK - TARUN JAIN & VK OHRICHAPTER - FREQUENCY DIAGRAMS - HISTOGRAM, POLYGON AND OGIVEEXERCISE - EXERCISE NCERT
7 Videos
- MEASURES OF CENTRAL TENDENCY - ARITHMETIC MEANBOOK - TARUN JAIN & VK OHRICHAPTER - MEASURES OF CENTRAL TENDENCY - ARITHMETIC MEANEXERCISE - Illustration
72 Videos
Similar Questions
Knowledge Check
Fisher’s Price Index Number is
A√P01(L)×P01(P)BP01(L)×P01(P)C√P01(L)×P01(P)×100D√P01(L)×P01(P)Which of the following is an ideal Index Number?
ALespeyreBBowleyCFisherDMarshall-Edgeworth
Find MC from the following data :

View SolutionFind MU from the following data :

View SolutionFind x from following data if the Value Index Number is 200

View SolutionFrom the following data, construct a price index number by using Fisher's Ideal Formula:
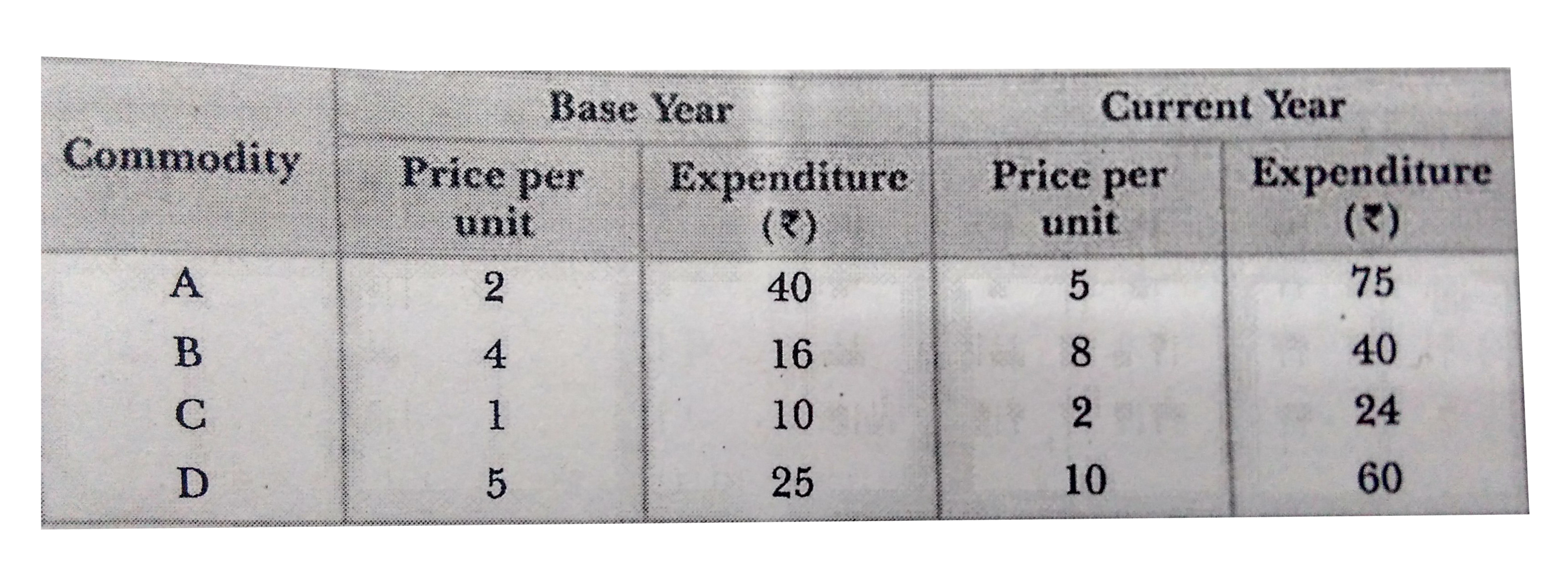
View SolutionConstruct index numbers of the following data by Fisher's Method:
View SolutionFind the mean of following data :

View Solution