ΔABC is an isosceles triangle with AB=AC, side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
Video Solution
Text Solution
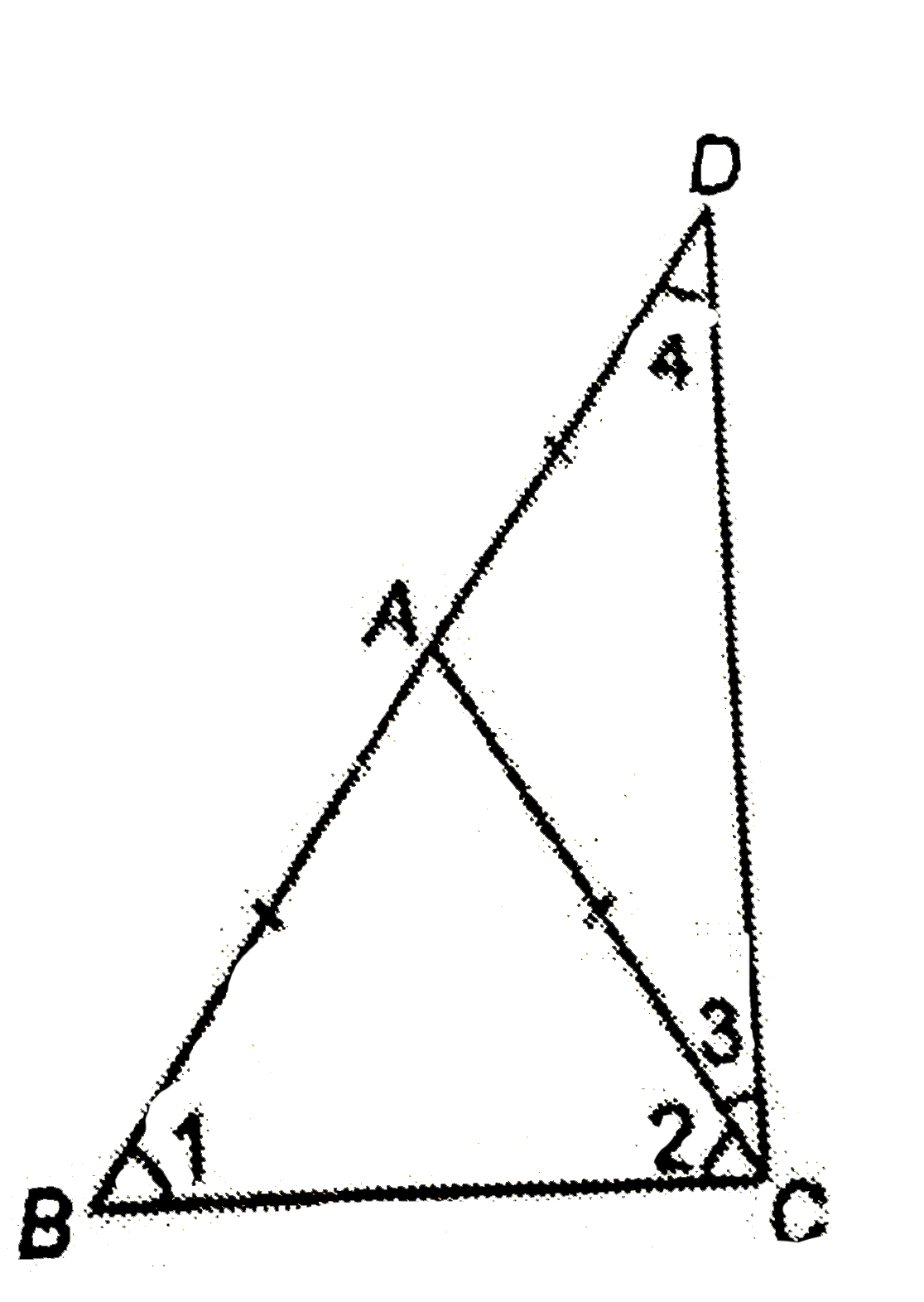
Given : ΔABC in which AB=AC. Side BA is produced to D such that AB =AD.
To prove : ∠BCD=90∘ i.e., ∠2+∠3=90∘
Proof : since AB=AC (given)
∴∠2=∠1 ...(1)
(angle opposite to equal sides are equal)
Also, AB=AC=AD (given)
∠3=∠4 (angles opposite to equal sides are equal) ...(2)
Now, in ΔBCD,
∠1+(∠2+∠3)+∠4=180∘ (angle sum property) ...(3)
⇒ ∠2+(∠2+∠3)+∠3=180∘ [from (1), (2) and (3)]
⇒ 2(∠2+∠3)=180∘
⇒ ∠2+∠3=90∘. Hence Proved.

|
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
Knowledge Check
ΔABC is an isosceles triangle with AB=AC, side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
A60∘B90∘C120∘Dcan't be determinedΔABC is an isosceles triangle with AB=AC, side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
A60∘B90∘C120∘Dcan't be determinedΔABC,AB=AC and BA is produced to D such that AC = AD. Then the ∠BCD is
A100∘B60∘C80∘D90∘
In the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
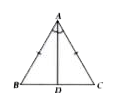
∠B=∠C
View SolutionIn the adjoining figure, ABC is an isosceles triangle in which AB = AC. Also, D is a point such that BD = CD. Prove that AD bisects ∠A and ∠D
View SolutionABC is an isosceles triangle with AB = AC. Side BA is produced to D such that AB=AD. Find the ∠BCD:
View SolutionABC is an isosceles triangle with AB = AC. Side BA is produced to D such that AB=AD. Find the ∠BCD:
View SolutionIf ΔABC is an isosceles triangle with ∠C=90°∘ and AC=5cm, then AB is :
View Solution
