The diagonal AC of a quadrilateral ABCD divides it into two triangles of equal areas. Prove that diagonal AC bisects the diagonal BD.
Step by step video, text & image solution for The diagonal AC of a quadrilateral ABCD divides it into two triangles of equal areas. Prove that diagonal AC bisects the diagonal BD. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHANChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Revision Exercise (very Short Answer Questions)
Explore 10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHANChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Revision Exercise (short Answer Questions)
Explore 10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHANChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Problems From NCERT/exemplar
Explore 12 Videos
- CIRCLE Book:NAGEEN PRAKASHANChapter:CIRCLE Exercise:Revision Exercise (long Answer Questions )
Explore 5 Videos
Similar Questions
Knowledge Check
The diagonal BD of a quadrilateral ABCD bisects ∠Band∠D, then :
 AABCD=ADBCBADAB=BCCDCABBC=ADCDDAB=AD×BC
AABCD=ADBCBADAB=BCCDCABBC=ADCDDAB=AD×BCABCD is a quadrilateral whose diagonals AC divides it into two parts, equal is area. Then, ABCD is
Aa rectangleBa ||gmCa rhombusDall of theseAsserion (A) : The diagonals of a ||gm divide it into four triangle of equal area.
Reason (R ) : A diagonal of a ||gm divides it into two triangle of equal area.ABoth Assertion (A) and Reason (R ) are true and Reason (R ) is a correct explansion of Assertion (A).BBoth Assertion (A) and Reason (R ) are true but Reason (R ) is not a correct explansion of Assertion (A).CAssertion (A) is true and Reason (R ) is false.DAssertion (A) is false and Reason (R ) is true.
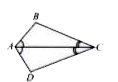
In Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
View SolutionIn the figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.
View SolutionIf the diagonals AC, BD of a quadrilateral ABCD, intersect at O, and separate the quadrilateral into four triangles of equal area, show that quadrilateral ABCD is a parallelogram.
View SolutionThe diagonals AC and BD of a quadrilateral ABCD intersect at point 'O'. If BO = OD, then prove that the areas of ΔABCandΔADC are equal
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way thatar(AOD)=ar(BOC).Prove that ABCD is a trapezium.
View Solution
