If AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in area. If G is the mid-point of median AD, prove that ar (BGC)=2ar ( AGC)
Proof : Since, AD is the median of ΔABC
Therefore, BD=DC
BD×AM=DC×AM
12(BD×AM)=12(DC×AM)
Area(ΔABD)=Area(ΔACD) ...(i)
Now, In ΔBGC,
GD is the median .
Therefore, Area (ΔBGD)=Area(ΔCGD) ...(ii)
Also, In ΔACD, CG is the median .
Therefore, Area(ΔAGC)=Area(ΔCGD) ...(iii)
From (i), (ii) and (iii) we have Area (ΔBGD)=Area(ΔAGC)
But, Area (ΔBGC)=2Area(ΔBGD)
Therefore, Area(ΔBGC)=2Area(ΔAGC)
. Hence, proved
Topper's Solved these Questions
Similar Questions
In Figure, ABCD and PQRC are rectangles and Q is the mid-point of AC . Prove that DP=PC (ii) PR=12 AC
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
View SolutionIn A ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (RQC)=38 ar ( ABC)
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=14ar(ABC)
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F Prove that: ar(FED)=18ar(AFC)
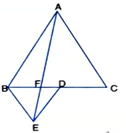
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BFE)=ar(AFD)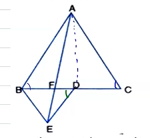
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=12ar(BAE)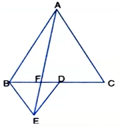
View SolutionIn Figure, ABC and BDE are two equilateral triangls such that D is the mid-point of BC.AE intersects BC in F. Prove that: ar ( BFE)= 2 ar (EFD)
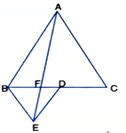
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View Solution