Find the distance of the line $4 x + 7 y + 5 = 0$ from the point $(1, 2)$ along the line $2 x - y = 0$ .

Video Solution

Text Solution

Verified by Experts

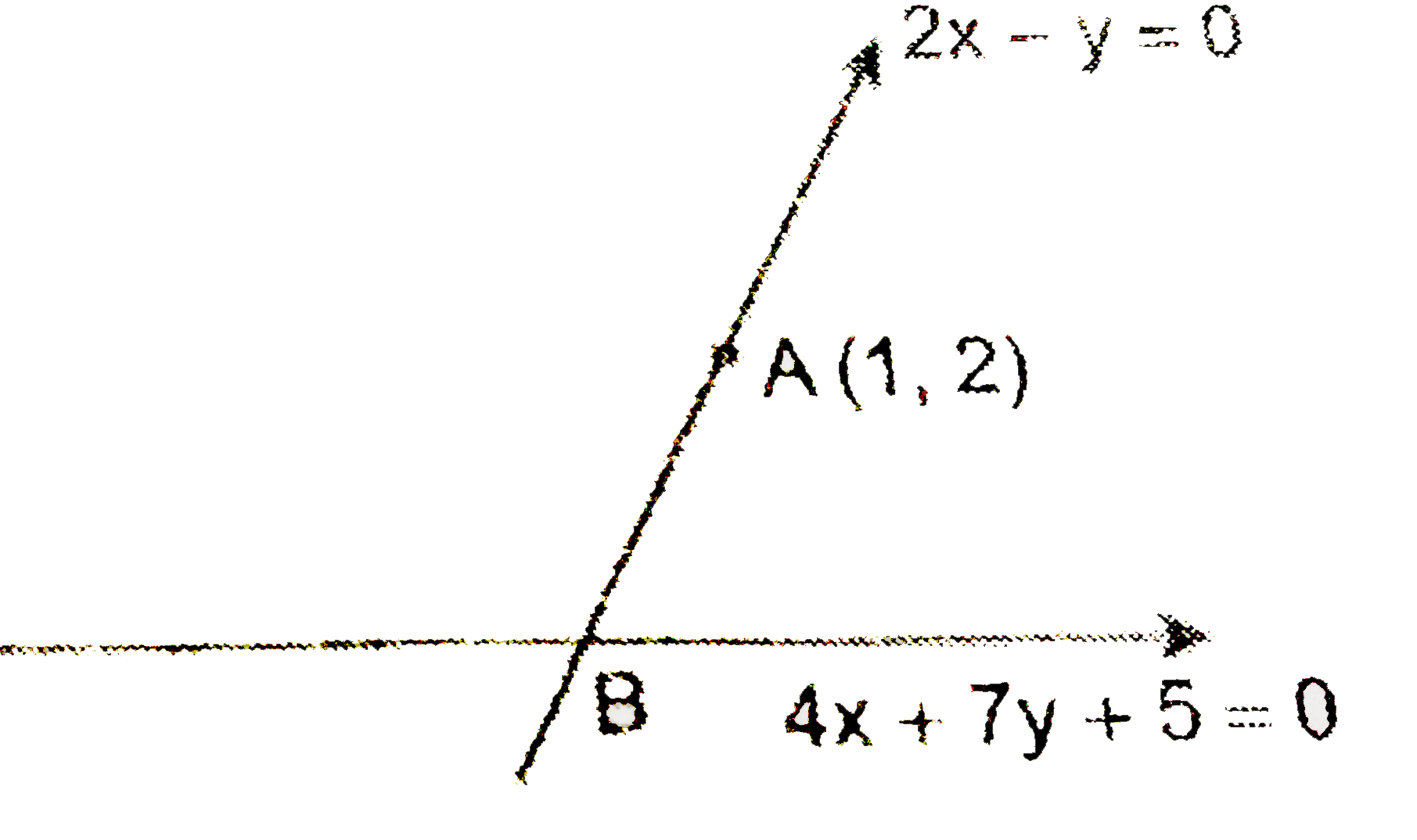
Given lines, $4 x + 7 y + 5 = 0$ …… $(1)$
and $2 x - y = 0$ ……. $(2)$
Here, equation $(2)$ passes through the point $A (1, 2)$ .
Solving equations $(1)$ and $(2)$ ,
$x = \frac{- 5}{18}$ and $y = - \frac{5}{9}$
$∴$ Point of intersection $B = (\frac{- 5}{18}, \frac{- 5}{9})$
Now, $A B = \sqrt{{(1 + \frac{5}{18})}^{2} + {(2 + \frac{5}{9})}^{2}}$
$= \sqrt{\frac{529}{324} + \frac{529}{81}} = \sqrt{\frac{529}{324} (1 + 4)}$
$= \frac{23 \sqrt{5}}{18}$ unit.

Updated on:21/07/2023

|

Class 11 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

The distance of the line $2 x + 3 y - 5 = 0$ from the point (3, 5) along the line $5 x - 3 y = 0$ in units is
A $\frac{2 \sqrt{34}}{21}$
B $\frac{16}{21}$
C $\frac{4 \sqrt{34}}{21}$
D $\frac{3 \sqrt{43}}{21}$

NAGEEN PRAKASHAN-STRAIGHT LINES-Exercise

Home
Ask Doubt
Profile