Find the direction in which a straight line must be drawn through the point $(- 1, 2)$ so that its point of intersection with the line $x + y = 4$ may be at a distance of $3$ units from this point.

Text Solution

Verified by Experts

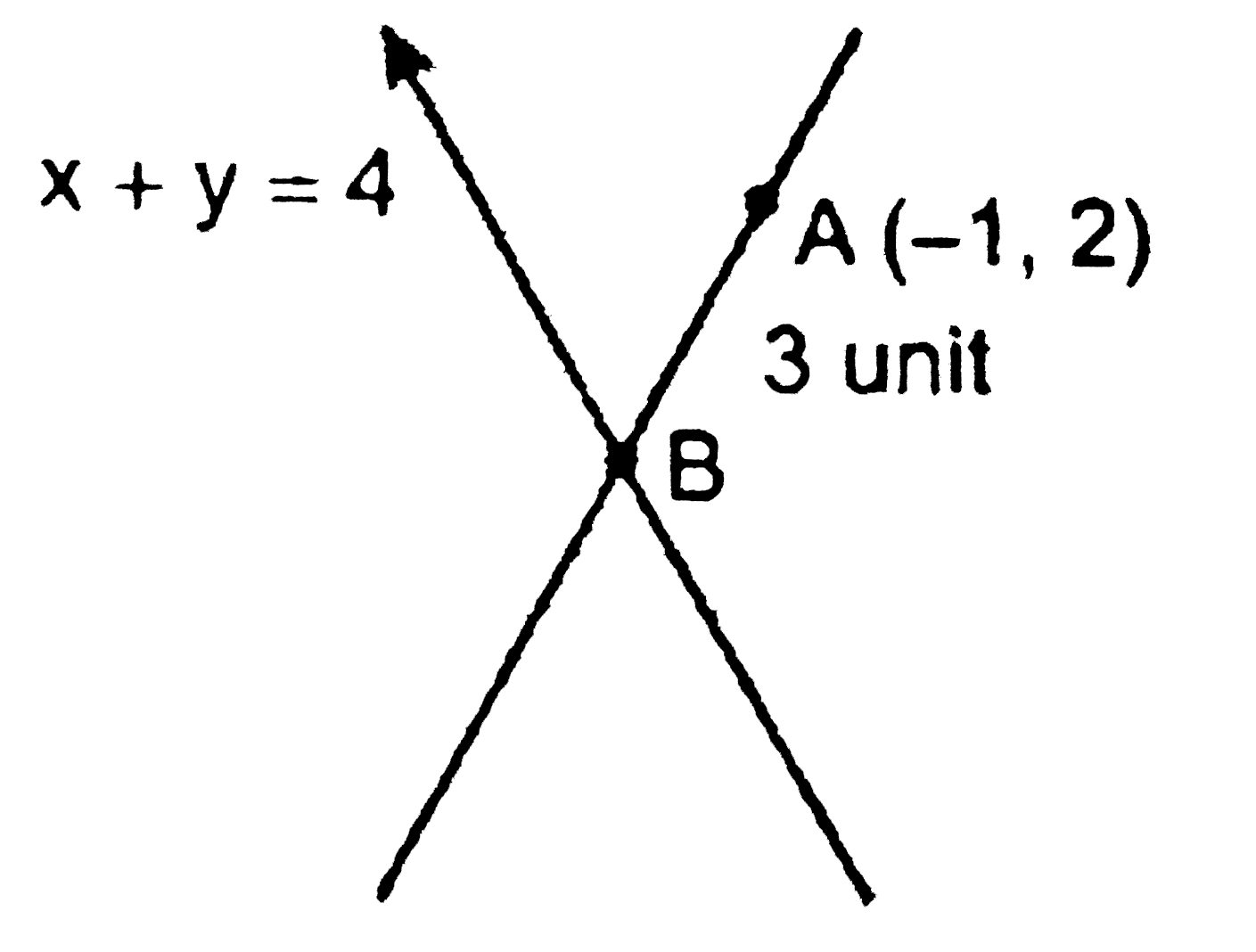
Let the slope of required line passing through the point $(- 1, 2)$ is $m$ .
$, .$ Equation of line is,
$y - 2 = m (x + 1)$
$\Rightarrow m x - y = - 2 - m$ ……. $(1)$
Given line is, $x + y = 4$ …….. $(2)$
Solving we get
$x = \frac{2 - m}{m + 1}$ and $y = \frac{5 m + 2}{m + 1}$
$∴$ Point of intersection is , $B = (\frac{2 - m}{m + 1}, \frac{5 m + 2}{m + 1})$
Given that $A B = 3$ units
$\Rightarrow \sqrt{{(\frac{2 - m}{m + 1} + 1)}^{2} + {(\frac{5 m + 2}{m + 1} - 2)}^{2}} = 3$
$\Rightarrow \sqrt{\frac{{(3)}^{2} + {(3 m)}^{2}}{{(m + 1)}^{2}}} = 3$
$\Rightarrow 3^{2} + 9 m^{2} = 9 {(m + 1)}^{2}$
$\Rightarrow 9 + 9 m^{2} = 9 m^{2} + 18 m + 9$
$\Rightarrow 4 m + 18 m = 0$
$\Rightarrow m = 0$
Now, $m = 0$ then $tan θ = 0 \Rightarrow θ = 0^{\circ}$
$\Rightarrow$ Line is parallel to $x$ -axis.

Updated on:21/07/2023

The direction in which a straight line must be drawn through the point (1,2) so that its point of intersection with the $x + y = 4$ may be at a distance $\frac{\sqrt{6}}{3}$ from theis point is
A $30^{\circ}, 60^{\circ}$
B $15^{2}, 75^{\circ}$
C $∣ ∣$ to x-axis
D|| to y-axis
In what direction a line be drawn through the point (1,2) . So that its point of intersection
with the line x+y=4 is at a distance $\sqrt{6} / 3$ from the given point ?
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $75^{\circ}$