Show that the products of the corresponding terms of the sequence a,ar,ar2,…arn−1 and A,AR,AR2,…ARn−1 from a G.P. and find the common ratio.
The correct Answer is:N/a
First sequence : a,ar,ar2,…arn−1
Second sequence :A,AR,AR2,….ARn−1
Sequence formed by the product of corresponding term of two sequences.
aA,aArR,aAr2R2,…aArn−1Rn−1
≡aA,aA(rR),aA(rR),….,aA(rR)n−1
Here a2a1=a3a2=rR
Therefore, this sequence is a G.P and its common ratio is rR.
∴ Common ratio=rR
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9.410videos
SEQUENCE AND SERIES
- BOOK - NAGEEN PRAKASHANCHAPTER - SEQUENCE AND SERIESEXERCISE - Miscellaneous Exercise32videos
SEQUENCE AND SERIES
- BOOK - NAGEEN PRAKASHANCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9.218videos
SEQUENCE AND SERIES
- BOOK - NAGEEN PRAKASHANCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE12videos
RELATIONS AND FUNCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - SETSEXERCISE - MISC Exercise16videos
SETS
Similar Questions
Show that the products of the corresponding terms of the sequences a, ar,ar2,.......,arn−1and A,AR,AR2,......,ARn−1,form a G.P, and find the common ratio.
View SolutionShow that the products of the corresponding terms of the sequences a,ar,ar2,...,arn−1anda,AR,AR2,....,ARn−1 form a G.P., and find the common ratio.
View Solution
Knowledge Check
- Question 1 - Select One
The sum upto n terms of the sequence log a, log ar, log ar2, …. Is
An2loga2rn−1Bn2logarn−1C3n2logarn−1D5n2loga2rn−1 - Question 2 - Select One
If a variate takes values a,ar,ar2,..arn−1 which of the relation between means hold
AAH=G2BA+H2=GCA>G>HDA=G=H - Question 3 - Select One
Let sum of ten numbers a,ar,ar2,...Ar9 is 18 and sum of their reciprocal is 6 then product of these ten numbers is.
A324B343C243D724
Show that the products of the corresponding terms o the sequences a, ar, ar2,.., arn−1 and A, AR, AR2, , ARn−1 form a G.P. and find the common ratio.
View SolutionProve that the sum of n terms of the reciprocals of the terms of the series a,ar,ar2,… is 1−rna(1−r)rn−1
View SolutionProve that the nth term of the GP with first term a and common ratio r is given by an=arn−1
View SolutionWhat ar the oxidative ozonolysis products of
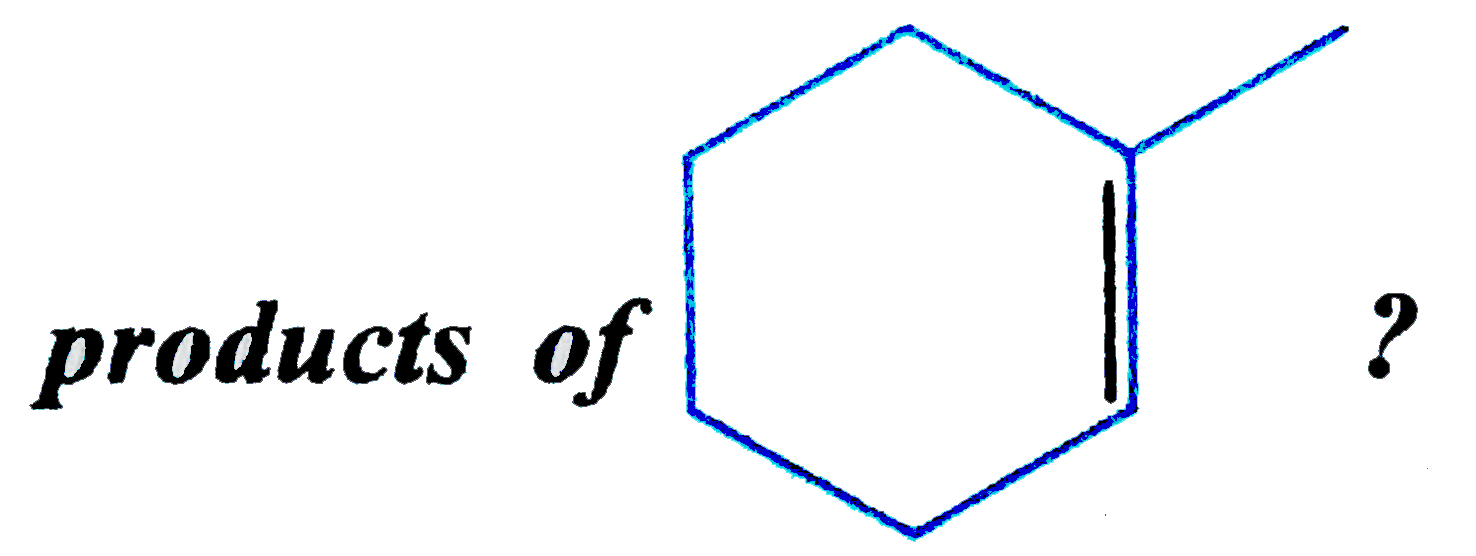 View Solution
View SolutionIf a,ar,ar2,ar3,....... are in G.P,then the sum of infinite terms of GP, if |r|<1=
View Solution

