If C0,C1,C2,...Cn are the binomial coefficients in the expansion of (1+x)n then prove that: C0+C12+C23+……+Cnn+1=2n+1−1n+1
The correct Answer is:N/a
L.H.S.=C0+C12+C23+….+Cnn+1
=1+n2+n(n−1)∣2.3–––+....+1n+1
=1n+1[(n+1)+(n+2)n∣2–
+(n+1)n(n−1)∣3–+.....+1]
=1n+1[{1+(n+1)+(n+1)n∣2–
+(n+1)n(n−1)∣3–+......+1}−]
=1n+1[{.n+1C0+n+1C1+n+1C2
+n+1C3+......+n+1Cn+1}−1]
=1n+1[2n+1−1]
=2n+1−1n+1=R.H.S. Hence Proved
Topper's Solved these Questions
Similar Questions
Knowledge Check
If C0,C1,C2,...,Cn are binomial coefficients
in the expansion of (1+x)n, then the value of
C0−C12+C23−C34+...+(−1)nCnn+1 isA0B1n+1C22n+1D−1n+1If C0,C1,c2,...,Cn denote the binomial coefficients in the expansion of (1+x)n, then
C0+C12+C23+...+Cnn+1or,n∑r=0Crr+1A2n+1+1n+1B2n+1−1n+1C2n+1n+1D2n−1n+1
If C0,C1,C2,…,Cn are the binomial coefficients
in the expansion of (1+x)n , prove that
(C0+2C1+C2)(C1+2C2+C3)…(Cn−1+2Cn+Cn+1)
(n−2)n(n+1)!n∏r=1(Cr−1+Cr).
View SolutionIf C0,C1,C2,…,Cn are the binomial coefficients
in the expansion of (1+x)n , prove that
(C0+2C1+C2)(C1+2C2+C3)…(Cn−1+2Cn+Cn+1)
(n−2)n(n+1)!n∏r=1(Cr−1+Cr).
View SolutionIn C0,C1C2….Cn are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
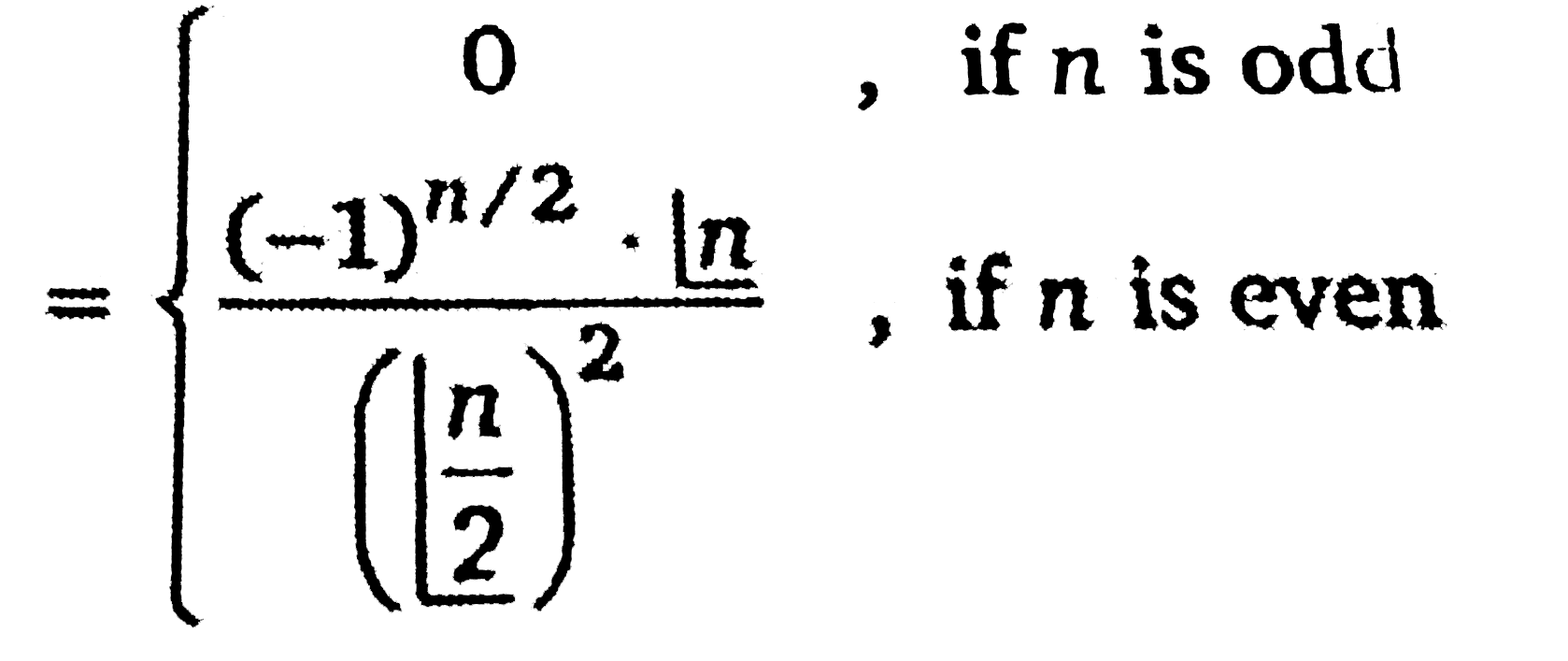
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
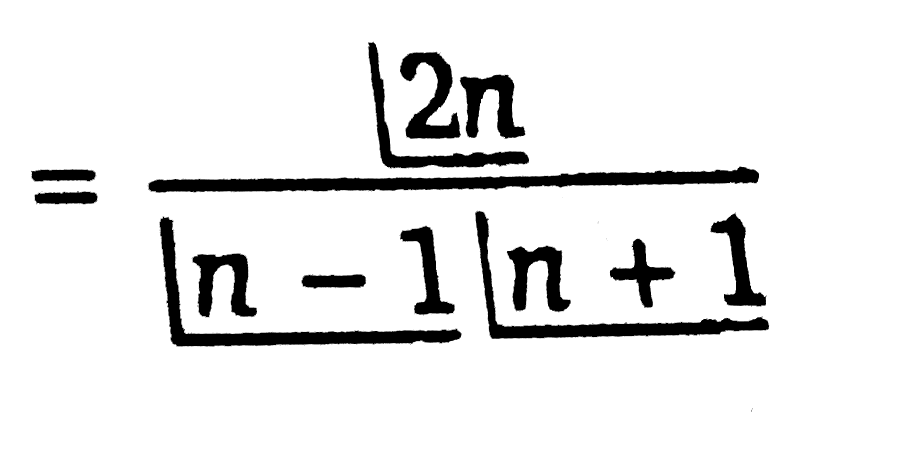
View SolutionIf C0,C1,C2………Cn are the binomial coefficient in the expansion of (1+x)n then prove that:
C20+C21+C22+……..+C2n=∣2–n|n––|n––
View SolutionIf C0,C1,C2………Cn are the binomial coefficient in the expansion of (1+x)n then prove that:
C20+C21+C22+……..+C2n=∣2–n|n––|n––
View SolutionIf C0,C1,C2,...,Cn denote the binomial coefficientsin the expansion of (1+x)n, then C02−C13+C24−C35+........+(−1)nCnn+2=
View Solution
