ifC0C1C2,……Cn are the binomial coefficients in the expansion of (1+x)n then prove that:
C0C2+C1C3+C2C4+……+Cn−2Cn=∣2–n|n––−2|n––+2
Video Solution
Text Solution
The correct Answer is:N/a
(1+x)n=c0+C1.x+C2.x2+C3.x3+......+Cn.xn
and (x+1)n=C0.xn+C1.xn+C1.xn−1+C2.xn−2
+C3.xn−3+…..+Cn
Now (1+x)2n)=(C0+C1.x+C2.x2+…+Cn.xn)
(C0.xn+C1.xn−1+C2.xn−2
+C3.xn−3.....+Cn)
Now C0C2+C1C3+C2C4+.....+Cn−2Cn= Coefficient of xn−2 in the expansion of (1+x)2n
∴ In the expansion of (1+x)2n
Tr+1=2nCr.(1)2n−r.xr
=2nCr.xr
∴ Coefficient of xn−2=2nCn−2=∣2–n∣∣n−2––––––∣∣n+2––––––
Therefore
C0C2+C1C3+C2C4+......+Cn−2Cn=∣2–n∣∣n−2––––––∣∣n––+2
Hence Proved.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If C0,C1,C2,…,Cn denote the binomial coefficients
in the expansion of (1+x)n, then
C02+2C12+3C22+...+(n+1)Cn2=A(2n+1)2nCnB(2n−1)2nCnC(n2+1)2nCnD(n2+1)2n−1Cn - Question 2 - Select One
If C0,C1,C2,…,Cn denote the binomial
coefficients in the expansion of (1+x)n , then n∑r=0n∑s=0CrCs=A2nBn2nC22nD2nCn - Question 3 - Select One
If C0,C1,C2,…,Cn denote the binomial
coefficients in the expansion of (1+x)n, then n∑r=0n∑s=0(Cr+Cs)A(n+1)2B(n+1)2n+1Cn2nDn2n+1
In C0,C1C2….Cn are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
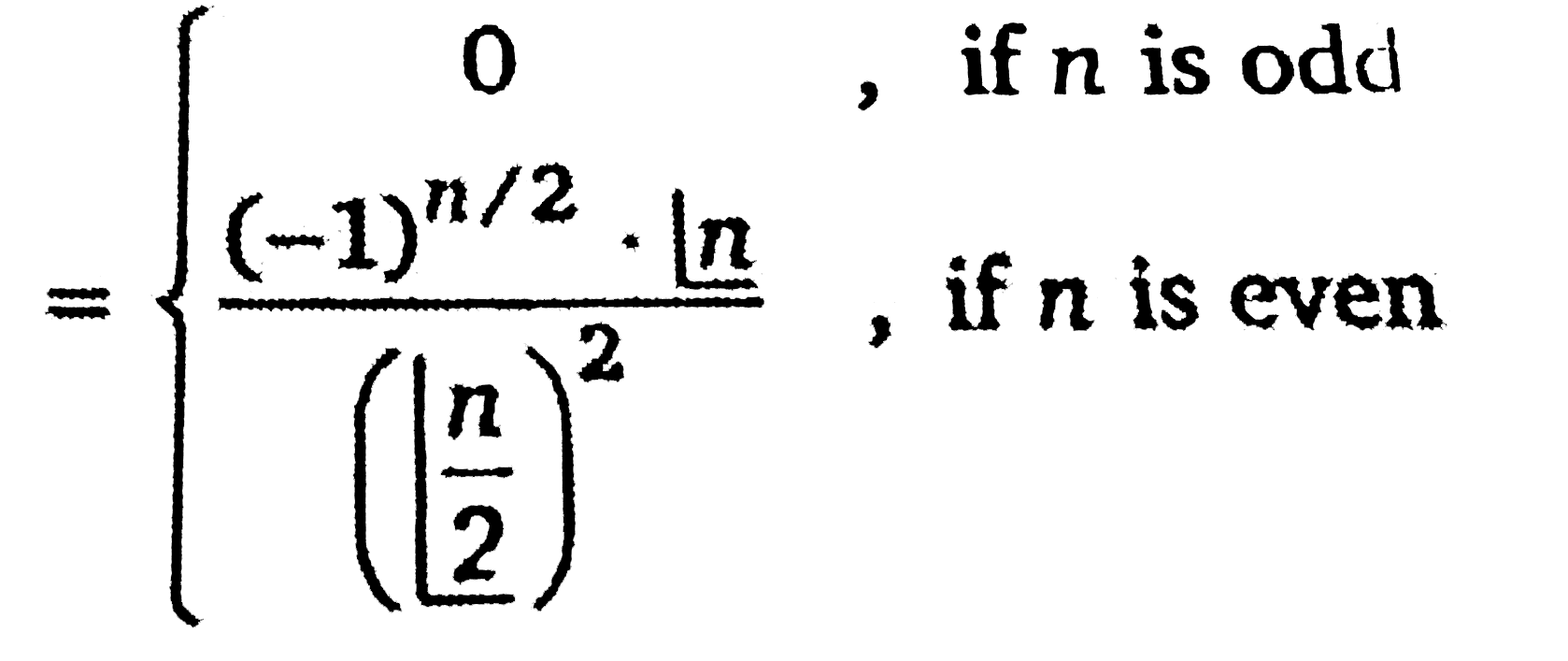
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
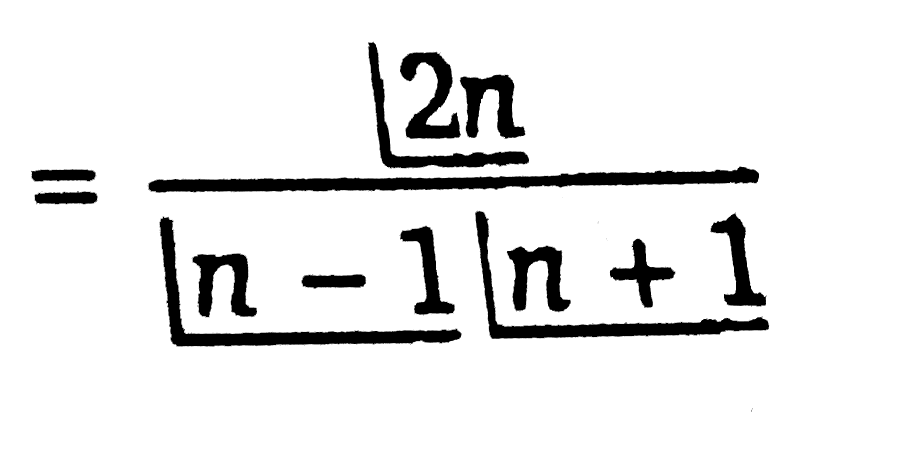 View Solution
View SolutionIf C0,C1,C2,…,Cn are the binomial coefficients
in the expansion of (1+x)n , prove that
(C0+2C1+C2)(C1+2C2+C3)…(Cn−1+2Cn+Cn+1)
(n−2)n(n+1)!n∏r=1(Cr−1+Cr).View SolutionIf CoC1,C2,.......,Cn denote the binomial coefficients in the expansion of (1+x)n, then the value of n∑r=0(r+1)Cr is
View SolutionIf C0,C1,C2,.......,Cn denote the binomial coefficients in the expansion of (1+1)n, then ∑0≤r∑<s≤n(Cr+Cs)
View SolutionIf C0,C1,C2,…,Cn are the coefficients in the expansion of (1+x)n, then what is the value of C1+C2+C3+….+Cn ?
View Solution

