Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B (4, 5) and C (6, 3).
Equation of line AB,
y−0=5−04−2(x−2)
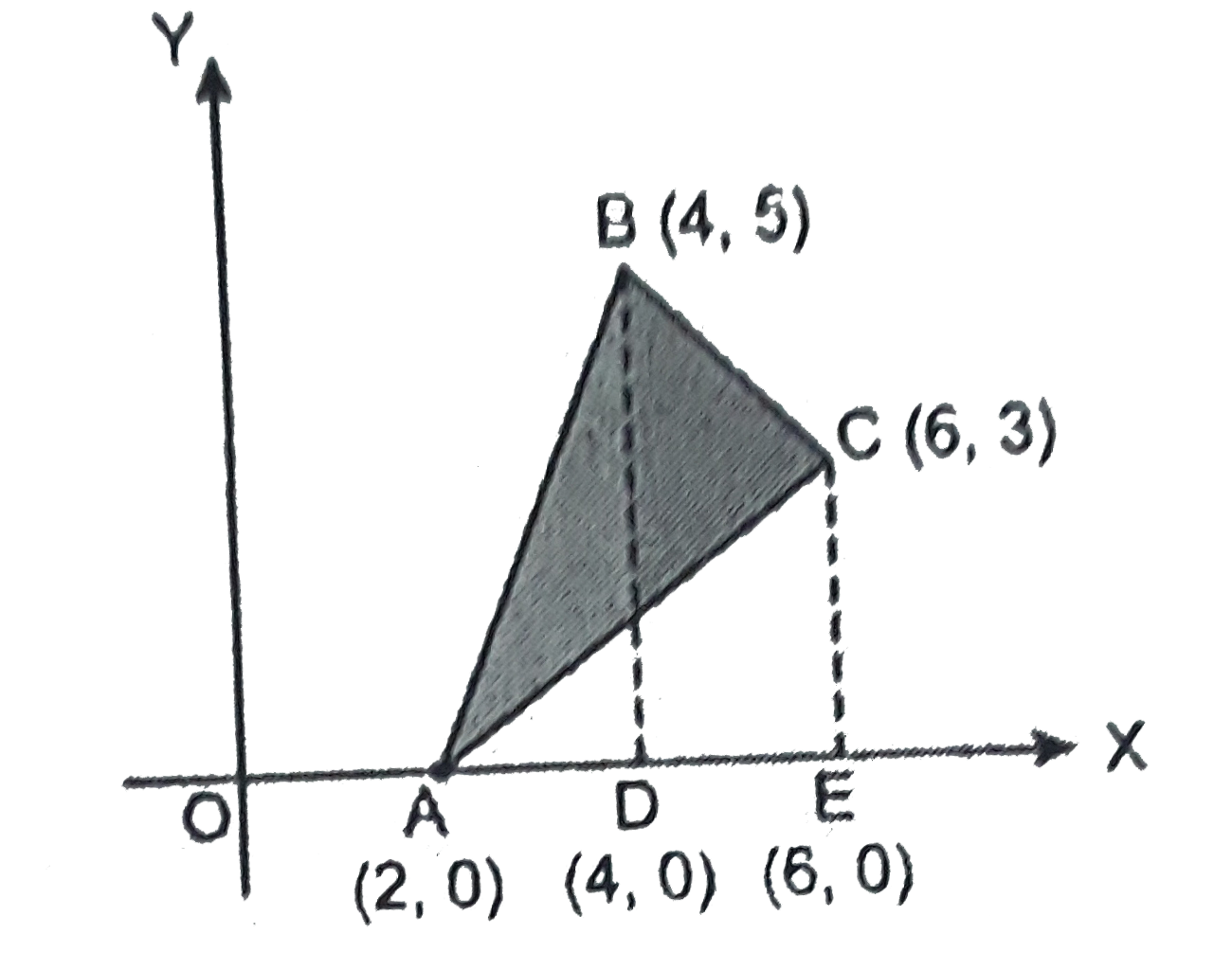
⇒y=52x−5
Equation of BC,
y−5=3−56−4(x−4)
⇒y=−x+9
Equation of CA, y−0=3−06−2(x−2)
⇒y=34x−32
ar(△ABC)=ar(ABCDA)+ar(DBCED)−ar(ACEA)
=∫42(52x−5)dx+∫64(9−x)dx−∫62(34x−32)dx
=[52x2−5x]42+[9x−x22]64−[38x−32x]62
=[(20−20)−(5−10)]+[(54−18)−(36−8)]−[(272−9)−(32−3)]
=5+36−28−92−32
=7 sq. units.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8.27videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise24videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHANCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise23videos
Continuity and Differentiability
Similar Questions
Knowledge Check
- Question 1 - Select One
The area of ΔABC whose vertices are A (2,5), B (4,7) and C(6,2) is
A7 sq. unitsB14 sq. unitsC21 sq. unitsD28 sq. units
Using integration, find the area of the triangle PQR, coordinates of whose vertices are P(2, 0), Q(4, 5) and R(6, 3).
View SolutionUsing the method of integration, find the area of the triangular region whose vertices are (2,−2),(4,3)and(1,2).
View SolutionUsing integration, find the area of the triangle ABC whose vertices are A(−1,1),B(0,5) and C(3,2).
View SolutionUsing intergration find the area of the area of the triangle whose vertieces are A(1,3), B(2,5)and C( 3,4)
View SolutionUsing integration find the area of region bounded by the triangle whose vertices are (1, 0), (2, 2) and (3, 1).
View SolutionFind the area of the quadrilateral whose vertices are A (0, 0), B (6, 0), C (4, 3) and D (0, 3).
View SolutionUsing integration find the area of region bounded by the triangle whose vertices are (1,0),(1,3)and(3,2).
View Solution

