Derive the expression for magnetic field at a point on the axis of a circular current loop. Solution in Kannada

Video Solution

Text Solution

Verified by Experts

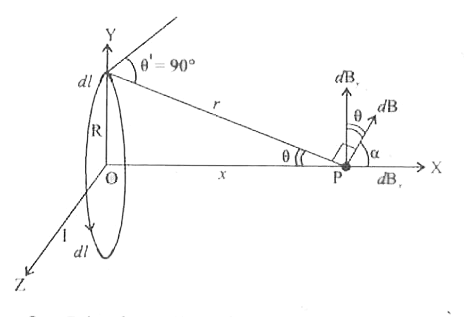
Let R be the radius of a current loop, carrying current I. Let R be a point on the axis of a conductor. Let dB be magnetic field at P, due to a current element .idl.
From the figure, $θ + a = 90^{\circ}$ , so that $α = 90^{\circ} - 0$ and $cos α = cos (90^{\circ} - 0)$
$sin θ = \frac{R^{2}}{{(R^{2} + x^{2})}^{\frac{1}{2}}}$ ...(1)
Let $d B_{x}$ be the horizontal component of dB.
Applying Biot-Savart.s law ,
We write
$d \to B = (\frac{μ_{0}}{4 π}) \frac{I (d \to l \times \to r)}{r^{3}}$
i.e., $d B = (\frac{μ_{0}}{4 π}) \frac{I r d l}{r^{3}} sin θ .$
where $θ . = 90^{\circ}$
i.e., $d B = (\frac{μ_{0}}{4 π}) \frac{I r d l}{r^{3}} = (\frac{μ_{0}}{4 π}) \frac{I d l}{r^{2}}$ ...(2)
Component of dB along the horizontal is
$d B_{x} = d B cos α$
or $d B_{x} = d B sin θ$
$= (\frac{μ_{0}}{4 π}) \frac{I d l}{r^{2}} sin θ$
By using (1) we write
$d B_{x} = (\frac{μ_{0}}{4 π}) \frac{I d l}{r^{2}} \frac{R}{r} = (\frac{μ_{0}}{4 π}) \frac{I d l R}{{(R^{2} + x^{2})}^{\frac{3}{2}}}$ ...(3)
or integrating
$B_{x} = \int d B_{x} = \int (\frac{μ_{0}}{4 π}) \frac{I R}{{(R^{2} + x^{2})}^{\frac{3}{2}}} d l$
i.e., $B_{x} = (\frac{μ_{0}}{4 π}) \frac{I R}{{(R^{2} + x^{2})}^{\frac{3}{2}}} d l$
i.e., $B_{x} = (\frac{μ_{0}}{4 π}) \frac{I R}{{(R^{2} + x^{2})}^{\frac{3}{2}}} (2 π R)$
where $\int d l = 2 π R$
or $B_{x} = (\frac{μ_{0}}{4 π}) ⎛ ⎜ ⎝ \frac{2 π I R^{2}}{{(R^{2} + x^{2})}^{\frac{3}{2}}} ⎞ ⎟ ⎠$ tesla
and $\to B = B_{x} ˆ i = (\frac{μ_{0}}{4 π}) ⎛ ⎜ ⎝ \frac{2 π I R^{2}}{{(R^{2} + x^{2})}^{\frac{3}{2}}} ⎞ ⎟ ⎠ ˆ i$ ,
$d B_{y} = 0$
For a circular loop , and at the centre , x=0
$\to B = (\frac{μ_{0}}{4 π}) (\frac{2 π I}{R}) ˆ i$
For a circular conductor containing n turns ,
$B_{x} ˆ i = (\frac{μ_{0}}{4 π}) \frac{2 π n I R^{2}}{{(R^{2} + x^{2})}^{\frac{3}{2}}} ˆ i$
and at the centre ,
$B_{0} ˆ i = (\frac{μ_{0}}{4 π}) (\frac{2 π n I}{R}) ˆ i$

Updated on:21/07/2023

|

Class 12 PHYSICS II PUC ANNUAL EXAMINATION QUESTION PAPER MARCH 2019

Topper's Solved these Questions

Similar Questions

SUBHASH PUBLICATION-II PUC ANNUAL EXAMINATION QUESTION PAPER MARCH 2019-QUESTION

Home
Ask Doubt
Profile