A straight wire of length π/2 m is bent into a circular shape.O is the center of the circle so formed and P is a point on its axis which is at a distance 3 times the from O .A current of 1A is passed through it Calculate the magnitude of the magnetic field at the points O and P .Solution in Kannada
Given : Circumference C=π2 m
I =IA n=1
Circumference of a circle =2πr
cancelpi/2=2cancelpir rArr r=1/4m
r=0.25 m
We known that B=μ02πnIr24π(r2+x2)3/2
At θ , x=0
B=(mu_02pinIr^(cancel2))/(4pir^(cancel31))
B=μ02πnI4πr=μ04π2πnIr=10−7×2×3.14×1×10.25
B=25.12×10−7 T
At Px=3r=3×0.25=0.75
B=μ04π2πnIr2(r2+x2)3/2=10−7×2×3.14×1×1×(0.25)2[(0.25)2+(0.75)2]3/2
B=0.3925×10−7[0.062+0.562]3/2=0.3925×10−7(0.624)3/2=0.3925×10−7(0.624)√0.625=0.3925×10−70.4933
B=0.795×10−7 T.
Topper's Solved these Questions
Similar Questions
A given coin has a mass of 3.0g . Calculate the nuclear energy that would be required to separate all the neutrons and protons from each other . For simplicity, assume that the coin is entirely made of .6329Cu atoms (of mass 62.92960 u)
View SolutionDerive an expression for potential energy of electric - di-pole placed in a n uniform electric field .
View SolutionA wire is bent in the form of a circular arc with a straight portion AB. Magnetic induction at O when current flowing in the wire, is

View SolutionA straight wire of length π/2 meter, is bent into a circular shape. If the wire were to carry a current of 5A, calculate the magnetic field, due to it, before bending, at a point distance 0⋅01 times the radius of the circle formed from it. Also calculate the magnetic field, at the centre of the circular loop formed, for the same value of current.
View SolutionA long straight wire carrying current I is bent into the shape as shown in the figure. The circular portion of the wire has radius (10//pi)m . The centre of this circle is at a distance 1m from the straight portion of the wire. What is the magnitude of the magnetic field at the centre of the circular portion? Given pi^2=10 .
View SolutionA thick straight wire of length πm is fixed at its midpoint and then bent in the form of a cricle. The shift in its centre of mass is
View SolutionA wire of mass m and length l is bent in the form of circular ring. The moment of inertia of the ring about its axis is
View SolutionO एक वृत्त्त की केंद्र है | P एक बाहुय बिन्दु है जो O से 13 से. मी की दूरी पर है | उस वृत्त्त की त्रिज्य 5 .से . मी है | तदनुसार P बिन्दु से वृत्त्त की स्पर्श रेखा के स्पर्श- बिन्दु तक की दूरी कितनी होगा |
View SolutionA wire is bent in the form of a circular arc of radius r with a straight portion AB. If the current in the wire is i , then the magnetic induction at point O is
View SolutionA straight wire of length pi //2 m is bent into a circular shape.O is the center of the circle so formed and P is a point on its axis which is at a distance 3 times the from O .A current of 1A is passed through it Calculate the magnitude of the magnetic field at the points O and P .
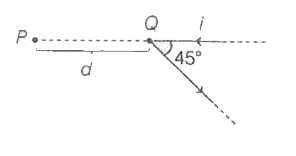
View SolutionA long straight wire carrying electric current i is bent at its mid-point to form an angle of 45∘ as shown in the figure. Magnetic field at a point P at a distance d from the point Q of bending is
View Solution((pi)/2)m A long straight wire is twisted in a circular shape. If there was a current of 5A in it, then before turning it, remove its magnetic field at some point 0.01 times the diameter of the circle made from it. Also find the magnetic field at the center of the circular loop designed for the same current value.
View SolutionA straight wire of length pi//2 m is bent into a circular shape. O is the centre of the circle formed and P is a point on its axis which is at a distance of 3 times the radius from O. A current of 1 A is passed throught it. Calculate the magnitude of the magnetic field at the point O and P .
View SolutionThe uniform wire of length I and mass m is bent in the form of circle , calculate moment of inertia of ring about an axis passing through its center and perpendicular to its length.
View SolutionA wire of length 1 m carrying current 1A is bent in the from of a circle .The magnitude of magnetic moment is :
View Solution
