In the given figure, the radius of curvature of curved surface for both the plano-convex and plano-concave lens is 10 cm and refractive index for both is 1.5. The location of the final image after all the refractions through lenses is
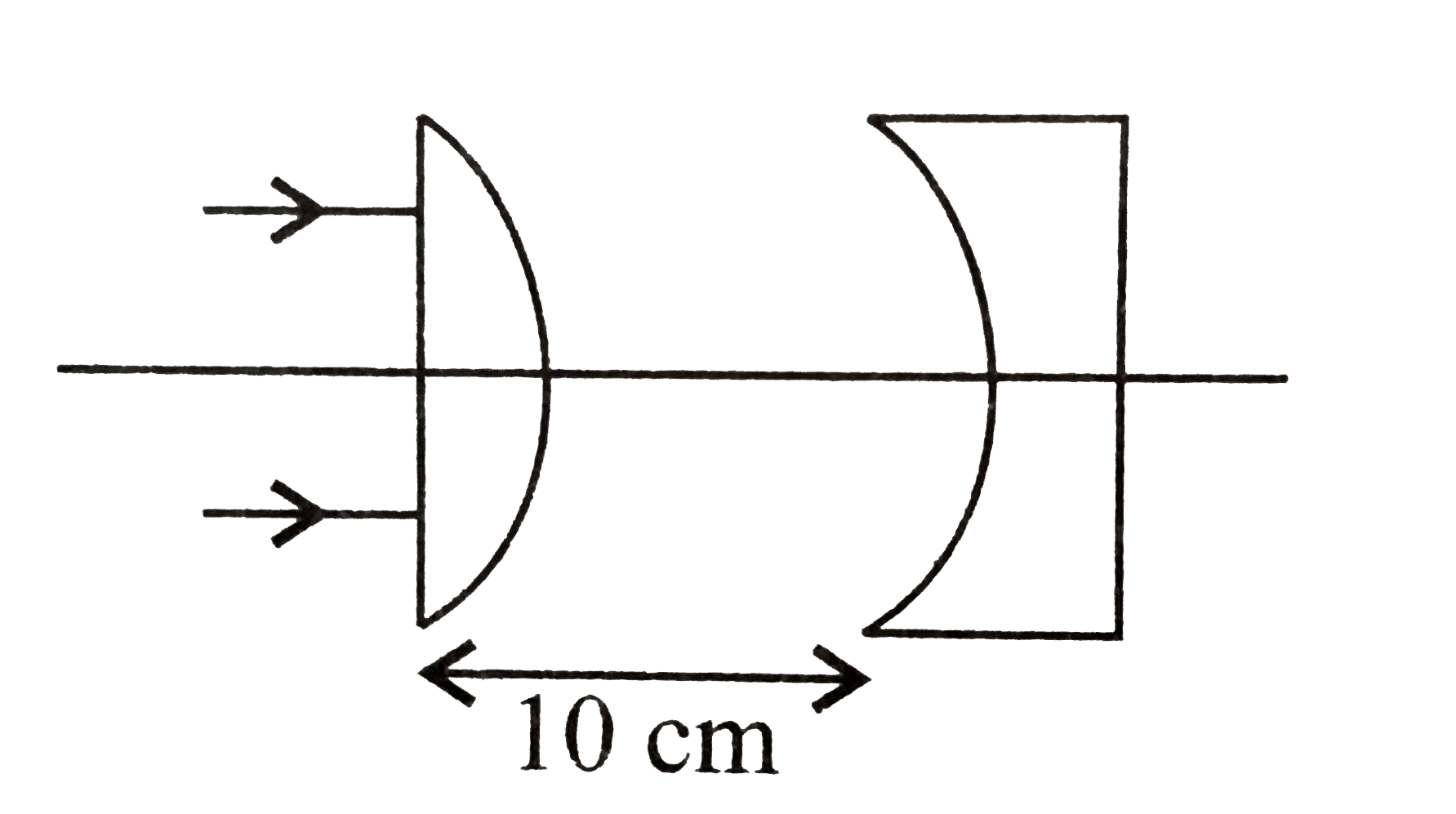
15 cm
20 cm
25 cm
40 cm
The correct Answer is:B
The focal length of the plano-convex lens is
1f=(1.5−1)(1+10−1∞)=120
Focal length of plano-concave lens is
1f=(1.5−1)(1∞−110)=−120
Since parallel beams are incident on the lens, its image from plano-concave lens will be formed at +20 cm from it (at the forcus) and will act as an object for the plano-concave lens. Since the two lens are at a distance of 10cm from each other, therefore, cor the next lens u=+10cm.
∴v=ufu+f=10×2010−20=20cm
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTIPSCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Refraction Through A Prism
9 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTIPSCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Some Natural Phenomena Due To Sunlight
2 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTIPSCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Total Internal Reflection
7 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTIPSCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTIPSCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
The radius of curvature of the convex surface of a thin plano-convex lens is 12 cm, and the refractive index of its material is 1.6. What is the power of lens ?
View SolutionThe radius of curvature of curved surface of a thin plano-convex lens is 10cm and the refractive index is 1.5. If the plano surface is silvered, then the focal length will be.
View Solution
Knowledge Check
The radius of curvature of the convex surface of a thin plano-convex lens is 15 cm and the refractive index of its material is 1.6. The power of the lens is
A+1DB−2DC+3DD+4DThe radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
Aact as a convex lens only for the object that lie on its curved side.Bact as a concave lens for the objects that lie on its curved side.Cact as a convex lens irrespective of the side on which the object lies.Dact as a concave lens irrespective of side on which the object lies.The radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
Aact as a convex lens only for the objects that lie on its curved side.Bact as a concave lens for the objects that lie on its curved side.Cact as a convex lens irrespective of the side on which the object lies.Dact as a concave lens irrespective of side on which the object lies.
Find the radius of curvature of the convex surface of a plano-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View SolutionFind the radius of curvature of the convex surface of a plano-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View SolutionThe radius of curvature of the convex surface of a thin plano-convex lens is 12 cm, and the refractive index of its material is 1.6. What is the power of lens ?
View SolutionThe radius of curvature of curved surface of a thin plano-convex lens is 10cm and the refractive index is 1.5. If the plano surface is silvered, then the focal length will be.
View SolutionThe radius of curvature of the convex face of a plano convex lens is 12cm and the refractive index of the material of the lends 1.5. Then, the focal length of the lens is
View Solution
