The radius of curvature of the convex surface of a thin plano-convex lens is 12 cm, and the refractive index of its material is 1.6. What is the power of lens ?
To find the power of the thin plano-convex lens, we will follow these steps:
Step 1: Identify the given values
- Radius of curvature of the convex surface (R1) = 12 cm
- Radius of curvature of the plane surface (R2) = ∞ (infinity)
- Refractive index (μ) = 1.6
Step 2: Use the lens maker's formula
The lens maker's formula for a thin lens is given by:
1f=μ−1(1R1−1R2)
Where:
- f is the focal length of the lens,
- R1 is the radius of curvature of the first surface (convex),
- R2 is the radius of curvature of the second surface (plane).
Step 3: Substitute the values into the formula
Substituting the known values into the formula:
1f=(1.6−1)(112−1∞)
Since 1∞=0, the equation simplifies to:
1f=0.6(112)
Step 4: Calculate 1f
Now, calculate 1f:
1f=0.6×112=0.612=6120=120
Thus, we find:
f=20 cm
Step 5: Convert focal length to meters
Since the power of the lens is expressed in diopters (D), we need to convert the focal length from centimeters to meters:
f=20 cm=0.2 m
Step 6: Calculate the power of the lens
The power (P) of the lens is given by the formula:
P=1f (in meters)
Substituting the value of f:
P=10.2=5 D
Final Answer
The power of the lens is 5 diopters.
---
- Radius of curvature of the convex surface (R1) = 12 cm
- Radius of curvature of the plane surface (R2) = ∞ (infinity)
- Refractive index (μ) = 1.6
The lens maker's formula for a thin lens is given by:
1f=μ−1(1R1−1R2)
Where:
- f is the focal length of the lens,
- R1 is the radius of curvature of the first surface (convex),
- R2 is the radius of curvature of the second surface (plane).
Substituting the known values into the formula:
1f=(1.6−1)(112−1∞)
Since 1∞=0, the equation simplifies to:
1f=0.6(112)
Now, calculate 1f:
1f=0.6×112=0.612=6120=120
Thus, we find:
f=20 cm
Since the power of the lens is expressed in diopters (D), we need to convert the focal length from centimeters to meters:
f=20 cm=0.2 m
The power (P) of the lens is given by the formula:
P=1f (in meters)
Substituting the value of f:
P=10.2=5 D
The power of the lens is 5 diopters.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXERCISE45videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - A)39videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assignment (Section - J) Aakash Challengers Questions7videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)4videos
PHYSICAL WORLD
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)10videos
SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )
Similar Questions
The radius of curvature of the convex face of a plano convex lens is 12cm and the refractive index of the material of the lends 1.5. Then, the focal length of the lens is
View SolutionFind the radius of curvature of the convex surface of a plan-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View Solution
Knowledge Check
- Question 1 - Select One
The radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
Aact as a convex lens only for the objects that lie on its curved side.Bact as a concave lens for the objects that lie on its curved side.Cact as a convex lens irrespective of the side on which the object lies.Dact as a concave lens irrespective of side on which the object lies. - Question 2 - Select One
In the given figure, the radius of curvature of curved surface for both the plano-convex and plano-concave lens is 10 cm and refractive index for both is 1.5. The location of the final image after all the refractions through lenses is
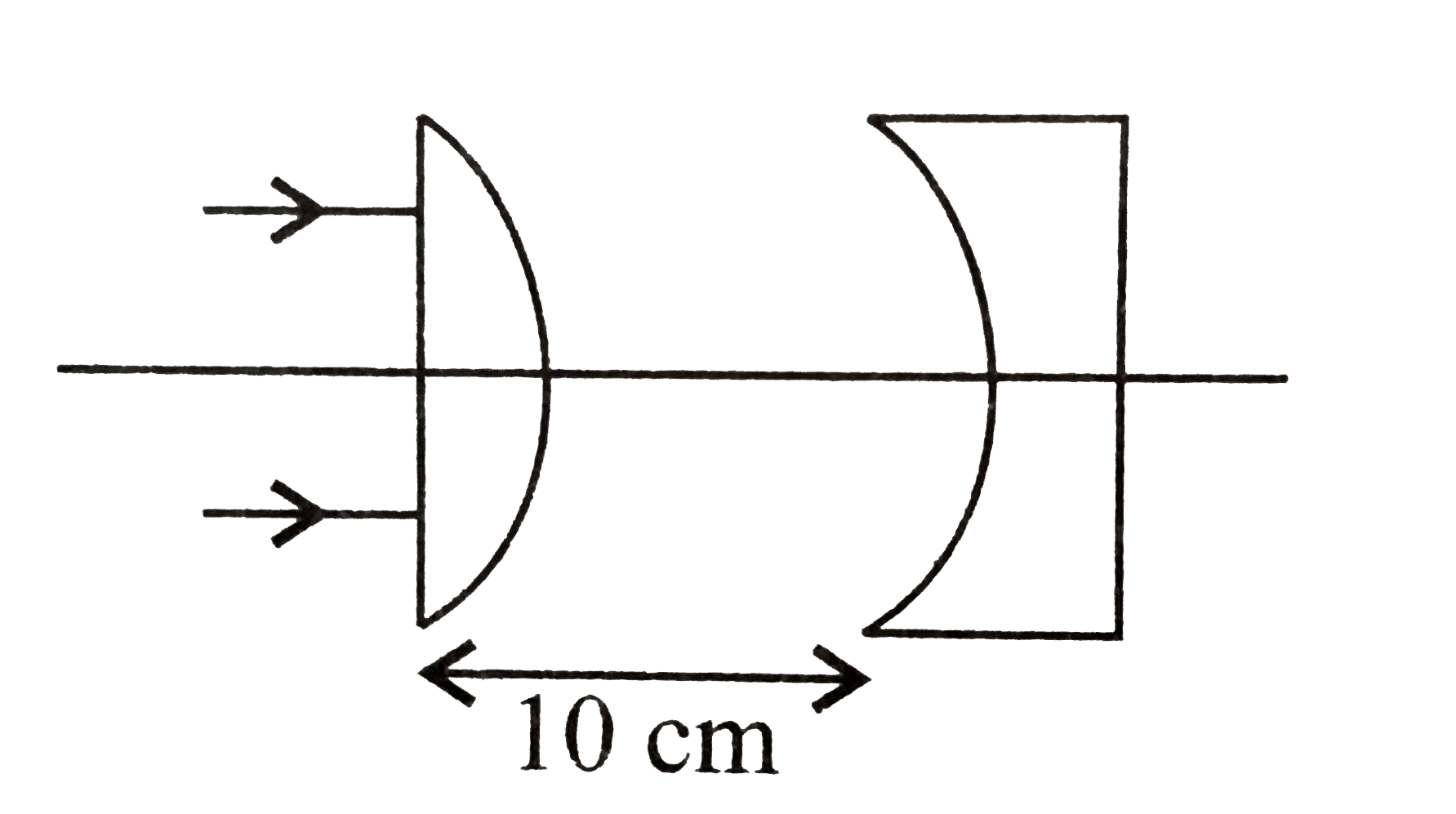 A15 cmB20 cmC25 cmD40 cm
A15 cmB20 cmC25 cmD40 cm
The radius of curvature of curved surface of a thin plano-convex lens is 10cm and the refractive index is 1.5. If the plano surface is silvered, then the focal length will be.
View SolutionThe effective focal length of the lens combination shown in figure is -60 cm. The radius of curvature of the curved surfaces of the plano-convex lenses are 12 cm each and refractive index of the material of the lens is 1.5. The refractive index of the liquid is
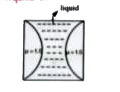 View Solution
View SolutionThe redius of curvature of the convex face of a plano-convex lens is 12cm and its refractive index is 1.5.
a. Find the focal length of this lens. The plane surface of the lens is now silvered.
b. At what distance form the lans will parallel rays incident on the convex face converge?
c. Sketch the ray diagram to locate the image, when a point object is places on the axis 20cm from the lens.
d. Calculate the image distance when the object is placed as in (c).View SolutionIf in a planoconvex lens, the radius of curvature of the convex surface is 10cm and the focal length is 30cm, the refractive index of the material of the lens will be
View SolutionIf in a plano-convex lens, the radius of curvature of the convex surface is 10 cm and the focal length of the lens is 30 cm , then the refractive index of the material of lens will be
View SolutionThe radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
View Solution

