A circle with center in the first quadrant is tangent to y=x+10,y=x−6, and the y−axis. Let (h,k) be the center of the circle. If the value of (h+k)=a+b√a where √a is a surd, find the value of a+b.
Step by step video & image solution for A circle with center in the first quadrant is tangent to y = x+10, y = x - 6, and the y- a x is. Let (h, k) be the center of the circle. If the value of (h + k) = a + b sqrta where sqrta is a surd, find the value of a +b. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A circle with center in the first quadrant is tangent to y=x+10,y=x−6, and the y−axis. Let (h,k) be the center of the circle. If the value of (h+k)=a+b√a where √a is a surd, find the value of a+b.
View SolutionA circle with center in the first quadrant is tangent to y=x+10,y=x-6 and the Y-axis. Let (p,q) be the centre of the circle. If the value oif (p+q)=a+b√a when a, b∈Q, then the value of |a-b| is
View Solution
Knowledge Check
x2+hxy+y2−6x−2y+k=0 is the equation of the circle and 2 is the radius of the circle, then find the values of h and k ?
Ah=0,k=−6Bh=0,k=6Ch=−3,k=6Dh=3,k=6
A circle with center in the first quadrant is tangent to y=x+10,y=x-6 and the Y-axis. Let (p,q) be the centre of the circle. If the value oif (p+q)=a+b√a when a, b∈Q, then the value of |a-b| is
View SolutionThe sides of a triangle ABC lie on the lines 3x+4y=0,4x+3y=0 and x=3 . Let (h,k) be the centre of the circle inscribed in △ABC. The value of (h+k) equals
View SolutionThe sides of a triangle ABC lie on the lines 3x+4y=0,4x+3y=0 and x=3 . Let (h,k) be the centre of the circle inscribed in △ABC. The value of (h+k) equals
View SolutionIn the following figure, O is the center of the circle. If x=40∘ and x:y=4:3, find the value of z.

View SolutionConsider a circle with the X and Y axes as tangents to it in the first quadrant.If the line x+3y=8 passes through the center of the circle and the radius of the circle equals k, then find the value of 3k
View Solution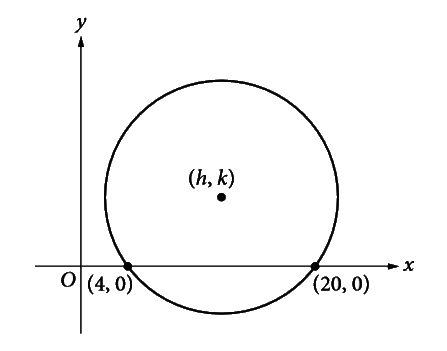
In the xy-plane above, the circle has center (h, k) and radius 10. What is the value of k ?
View SolutionA circle passes through the origin and has its center on y=x If it cuts x2+y2−4x−6y+10=0 orthogonally, then find the equation of the circle.
View Solution
