Instantaneous temperature difference between cooling body and the surroundings obeying Newton's law of cooling is $θ$ . Which of the following represents the variation of In $θ$ with time t?

ocr_image

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to analyze the situation using Newton's law of cooling. Let's break down the steps to find the variation of $ln θ$ with time $t$ .
1. Understand Newton's Law of Cooling:
According to Newton's law of cooling, the rate of heat loss of a body is directly proportional to the temperature difference between the body and its surroundings. Mathematically, this can be expressed as:
$\frac{d T}{d t} = - k (T - T_{s})$
where $T$ is the temperature of the cooling body, $T_{s}$ is the surrounding temperature, and $k$ is a positive constant.
2. Define Temperature Difference:
Let $θ = T - T_{s}$ . This represents the instantaneous temperature difference between the cooling body and the surroundings.
3. Rewrite the Equation:
Substituting $θ$ into the equation, we have:
$\frac{d θ}{d t} = - k θ$
4. Separate Variables:
We can rearrange the equation to separate the variables:
$\frac{d θ}{θ} = - k d t$
5. Integrate Both Sides:
Now, we integrate both sides. The left side integrates to $ln θ$ and the right side integrates to $- k t + C$ :
$\int \frac{d θ}{θ} = \int - k d t$
This gives us:
$ln θ = - k t + C$
6. Rearranging the Equation:
We can rearrange this equation to express $ln θ$ in terms of time $t$ :
$ln θ = - k t + C$
7. Identify the Relationship:
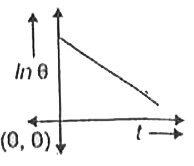
From the equation $ln θ = - k t + C$ , we can see that $ln θ$ decreases linearly with time $t$ . This means that as time increases, $ln θ$ will decrease.
8. Conclusion:
The relationship indicates that $ln θ$ varies linearly with time $t$ , which is a straight line with a negative slope.
Final Answer:
The variation of $ln θ$ with time $t$ is represented by a straight line with a negative slope.

Updated on:18/9/2024

Newton's law of cooling leads us to the following expression.
A $(θ - θ_{0}) = K t + C$
B $log (θ - θ_{0}) = K t + C$
C $log θ = K t + C$
D $θ = K θ_{0} + C$
As difference of temperature of body and surroundings increases, rate of cooling
Aincreases
Bdecreases
Cdoes not depend on it
Dincreases or decreases
Graph of rate of cooling against time is (assume Newton's law of cooling)
Astraight line
Bexponentially decreasing curve
Ccurve
Dparabola