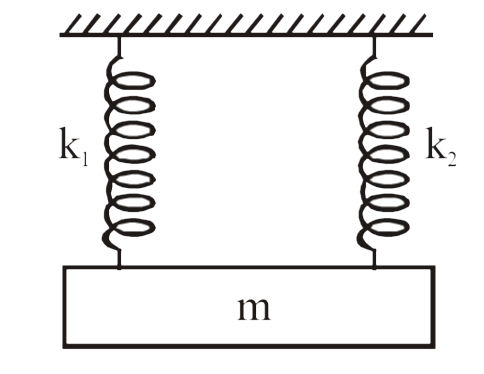
When a block of mass m is suspended separately by two different springs have time period t1 and t2. If same mass is connected to parallel combination of both springs, then its time period is given by :-
t1t2t1+t2
t1t2√t21+t22
√t1t2t1+t2
t1+t2
The correct Answer is:B
Step by step video, text & image solution for When a block of mass m is suspended separately by two different springs have time period t_(1)" and "t_(2). If same mass is connected to parallel combination of both springs, then its time period is given by :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Assignment (Section - B) (OBJECTIVE TYPE QUESTIONS)
30 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Assignment (Section C) (PREVIOUS YEARS QUESTIONS)
43 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Exercise
20 Videos
- NUCLEIBOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
5 Videos
Similar Questions
A mass is suspended separately by two different springs in successive order, then time periods is t1andt2 respectively. It is connected by both springs as shown in fig. then time period is t0. The correct relation is
View SolutionA mass is suspended separately by two springs and the time periods in the two cases are T1 and T2. Now the same mass is connected in parallel (K=K1+K2) with the springs and the time is suppose TP. Similarly time period in series is TS, then find the relation between T1,T2 and TP in the first case and T1,T2 and TS in the second case.
View Solution
Knowledge Check
A mass is suspended separately by two different springs in successive order then time periods is t1 and t2 respectively. If it is connected by both spring as shown in figure then time period is to, the correct relation is
 At20=t21+t22Bt−20=t−21+t−22Ct−10=t−11+t−12Dt0=t1+t2
At20=t21+t22Bt−20=t−21+t−22Ct−10=t−11+t−12Dt0=t1+t2A mass m is suspended separately by two different springs of spring constant k1 and k2 given the time period t1 and t2 respectively. If the same mass m is shown in the figure then time period t is given by the relation
 At=t1+t2Bt=t1t2t1+t2Ct2=t21+t22Dt−2=t−21+t−22
At=t1+t2Bt=t1t2t1+t2Ct2=t21+t22Dt−2=t−21+t−22T1,T2 are time periods of oscillation of a block when individually suspended to springs of force constants K1,K2 respectively. If same block is suspended to parallel combination fo same two springs. Its time period is
AT1+T2BT1+T22CT1T2T1+T2DT1T2√T21+T22
Periodic time of oscillation T1 is obtained when a mass is suspended from a spring and if another spring is used with same mass then periodic time of oscillation is T2 . Now if this mass is suspended from series combination of above springs then calculated the time period.
View SolutionA mass m is suspended from a weightless spring. The time period of oscillation of mass is 3 s . Calculate the value of m if on suspending an additional mass of 3kg, time period increases by 2 s.
View SolutionPeriodic time of oscillation T1 is obtained when a mass is suspended from a spring if another spring is used with same mass then periodic time of oscillation is T2. Now if this mass is suspended from series combination of above spring then calculate the time period.
View SolutionLet T1andT2 be the periods of springs A and B when mass M is suspended from one end of each spring. If both springs are taken in series and the same mass A is, suspended from the séries combination, the time period is T, then
View SolutionT1,T2 are time periods of oscillation of a block when individually suspended to springs of force constants K1,K2 respectively. If same block is suspended to series combination of same two springs, then it time period of oscillation.
View Solution
