A mass m is suspended from a weightless spring. The time period of oscillation of mass is 3 s . Calculate the value of m if on suspending an additional mass of 3kg, time period increases by 2 s.
To solve the problem, we will use the formula for the time period of a mass-spring system, which is given by:
T=2π√mk
where T is the time period, m is the mass, and k is the spring constant.
Step 1: Write the equations for the two scenarios
1. For the first scenario, where the time period T1=3 seconds:
T1=2π√mk⟹3=2π√mk
Squaring both sides:
9=4π2mk⟹9k=4π2m⟹k=4π2m9(Equation 1)
2. For the second scenario, where an additional mass of 3 kg is added and the time period increases to T2=5 seconds:
T2=2π√m+3k⟹5=2π√m+3k
Squaring both sides:
25=4π2m+3k⟹25k=4π2(m+3)(Equation 2)
Step 2: Substitute Equation 1 into Equation 2
Now we will substitute the expression for k from Equation 1 into Equation 2:
25(4π2m9)=4π2(m+3)
Step 3: Simplify the equation
Cancelling 4π2 from both sides (assuming π≠0) gives:
100m9=m+3
Step 4: Solve for m
To eliminate the fraction, multiply through by 9:
100m=9m+27
Rearranging gives:
100m−9m=27⟹91m=27⟹m=2791
Step 5: Final answer
Thus, the value of m is:
m=2716 kg
T1=2π√mk⟹3=2π√mk
Squaring both sides:
9=4π2mk⟹9k=4π2m⟹k=4π2m9(Equation 1)
T2=2π√m+3k⟹5=2π√m+3k
Squaring both sides:
25=4π2m+3k⟹25k=4π2(m+3)(Equation 2)
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Conceptual Questions
18 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - TOUGH & TRICKY PROBLEMS
9 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - PRACTICE PROBLEMS
15 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
The period of oscillation of a mass m suspended by an ideal spring is 2s. If an additional mass of 2 kg be suspended, the time period is increased by 1s. Find the value of m.
View SolutionA period of oscillation of a mass m kg is suspended by an ideal spring is 1.5s. If an additional mass 3kg be suspended, the time period is increased by 1s. Find the value of m.
View Solution
Knowledge Check
The time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A2π√m6kB2π√11m6KC2π√6m11KD2π√mKA mass of 1 kg is suspended from a spring. Its time period of oscillation on the earth is T. What will be its time periods at the centre of the earth?
AZeroBTC2TDInfiniteOne mass m is suspended from a spring. Time period of oscilation is T. now if spring is divided into n pieces & these are joined in parallel order then time period of oscillation if same mass is suspended.
A2π√n2mkB2π√n2kmC2π√mn2kD2π√kn2m
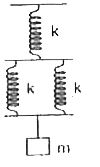
Calculate the period of oscillations of block of mass m attached with a set of springs as shown
View SolutionWhen a mass M is suspended from a spring, its period of oscillation is 2 second. If a mass 4 M is suspended from the same spring, then its period of oscillation will be
View SolutionIf the period of oscillation of mass m suspended from a spring is 2 s, then the period of mass 4 m will be
View SolutionWhen a block of mass m is suspended separately by two different springs have time period t1 and t2. If same mass is connected to parallel combination of both springs, then its time period is given by :-
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View Solution
