Two identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
Kq2l2+2 mg
Kq24l2+2 mg
Kq2l2
Kq24l2
To find the tension in the strings when two identical small bodies, each of mass m and charge q, are suspended from two strings of length l in an orbiting artificial satellite, we can follow these steps:
Step 1: Understand the System
In the artificial satellite, the effect of gravity is negligible (or zero), so the only forces acting on the charges are the tension in the strings and the electrostatic repulsion between the two charges.
Step 2: Identify Forces Acting on the Charges
Each charge experiences:
- Tension T acting along the string towards the fixed point.
- Electrostatic force F due to repulsion between the two identical charges.
Step 3: Calculate the Electrostatic Force
The electrostatic force F between two charges q separated by a distance R is given by Coulomb's law:
F=k⋅q1⋅q2R2
Here, k is Coulomb's constant, q1=q, and q2=q. The distance R between the two charges when they are in equilibrium in the satellite will be R=2l (since each string has length l and they are at the maximum distance apart).
Thus, we can write:
F=k⋅q⋅q(2l)2=k⋅q24l2
Step 4: Relate Tension and Electrostatic Force
In equilibrium, the tension T in the strings must balance the electrostatic force F:
T=F
Substituting the expression for F:
T=k⋅q24l2
Conclusion
The tension in the strings when the system is in an orbiting artificial satellite is given by:
T=k⋅q24l2
In the artificial satellite, the effect of gravity is negligible (or zero), so the only forces acting on the charges are the tension in the strings and the electrostatic repulsion between the two charges.
Each charge experiences:
- Tension T acting along the string towards the fixed point.
- Electrostatic force F due to repulsion between the two identical charges.
The electrostatic force F between two charges q separated by a distance R is given by Coulomb's law:
F=k⋅q1⋅q2R2
Here, k is Coulomb's constant, q1=q, and q2=q. The distance R between the two charges when they are in equilibrium in the satellite will be R=2l (since each string has length l and they are at the maximum distance apart).
F=k⋅q⋅q(2l)2=k⋅q24l2
In equilibrium, the tension T in the strings must balance the electrostatic force F:
T=F
Substituting the expression for F:
T=k⋅q24l2
The tension in the strings when the system is in an orbiting artificial satellite is given by:
T=k⋅q24l2
Similar Questions
Two identical spheres of mass m and charge q are suspended from a common point by two threads of the same length l and it is found that threads make an angle θ with the vertical when the spheres are in equilibrium . Calculate the value of q.
View SolutionTwo idential pith balls , each of mass m and charge +q. are suspended from a point with threads of length l each. If in equiilbrium state θ be the angle which each thread makes with vertical in equilibrium , find value of charge on each ball.
View Solution
Knowledge Check
Three identical point charges, each of mass m and charge q, hang from three strings as shown in fig. The value of q in term of m, L, and q is
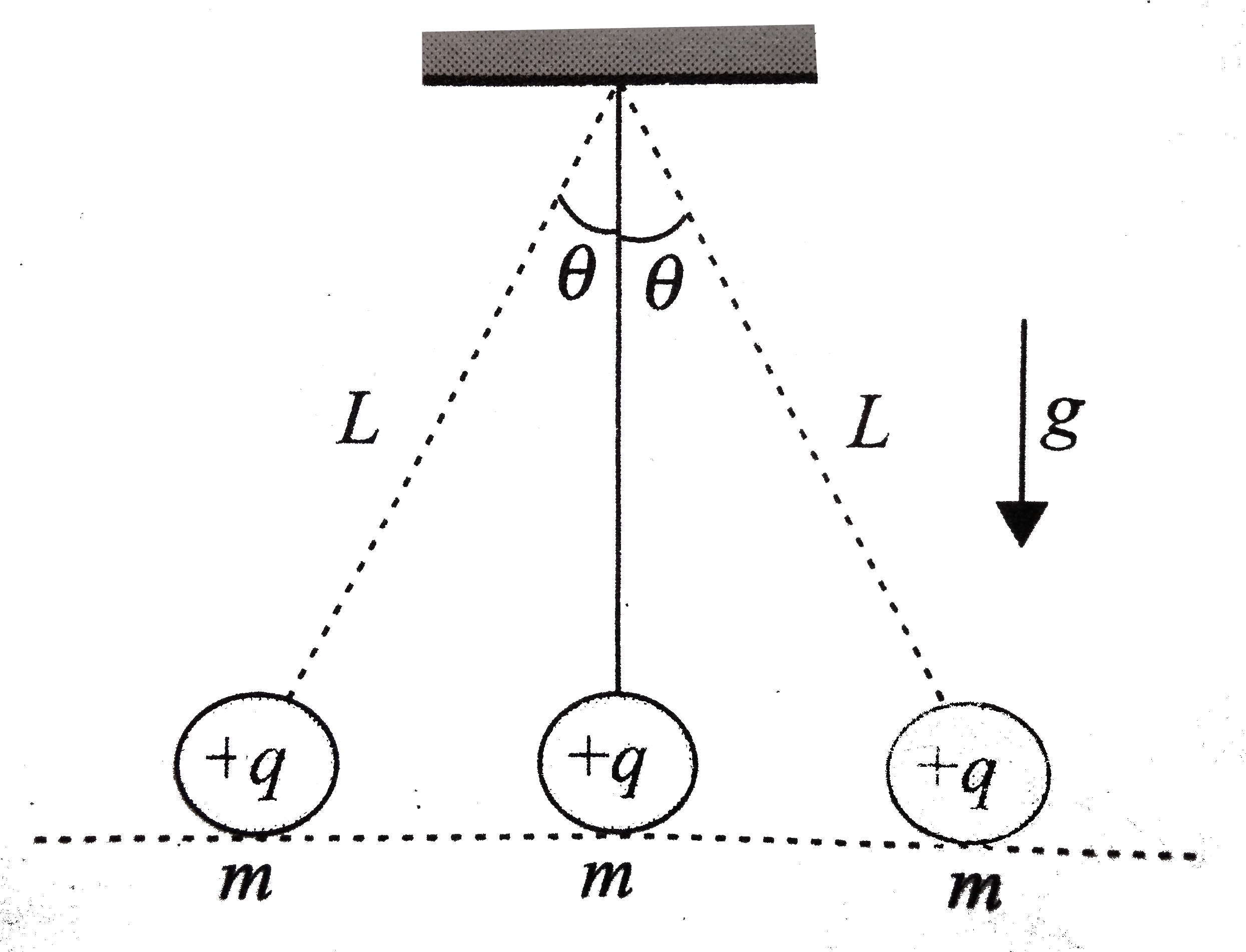 Aq=√(16/5)πε0mgL2sin2θtanθBq=√(16/15)πε0mgL2sin2θtanθCq=√(15/16)πε0mgL2sin2θtanθDnone of these
Aq=√(16/5)πε0mgL2sin2θtanθBq=√(16/15)πε0mgL2sin2θtanθCq=√(15/16)πε0mgL2sin2θtanθDnone of theseTwo small balls having equal positive charge Q (coulomb) on each are suspended by two insulated string of equl length L meter, from a hook fixed to a stand. The whole set-up is taken in satellite into space where there is no gravity (state of weightlessness). Then the angle between the string and tension in the string is
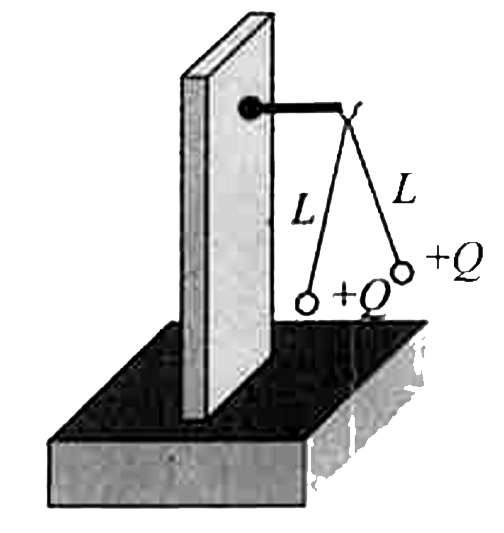 A180∘,14πε0.Q2(2L)2B90∘,14πε0.Q2L2C180∘,14πε0.Q22L2D180∘,14πε0.QL4L2
A180∘,14πε0.Q2(2L)2B90∘,14πε0.Q2L2C180∘,14πε0.Q22L2D180∘,14πε0.QL4L2Two small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
AQ24π∈0L2BQ28π∈0L2CQ212π∈0L2DQ216π∈0L2
Two small balls having equal poistive charges Q( coulomb) on each are suspended by two insulating strings of equal length L(metre) from a hook fixed to a stand. The whole set up is taken in a satellite into space where there is no gravity (state of weightlessness). The angle between the two strings is...............and the tenison in each string is...................newtons.
View SolutionTwo identical point charges q of mass m each are suspended through strings of equal length l from a common point of suspension. Find the charge q if angle subtended by the strings with the vertical is θ, when point charges are in a state of equilibrium.
View SolutionA uniform rod of mass m and length L is suspended through two vertical strings of equal lengths fixed at ends. A small object of mass 2m is placed at distance L/4 from the left end. Find the tensions in the two strings.
View SolutionTwo identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle 'θ' with the vertical ?
View SolutionTwo small balls, each having equal positive charge Q are suspended by two insulationg strings of equal length l from a hook fixed to a stand. It mass of each ball =m and total angle between the two strings is 60∘m, then find the charge on each ball.
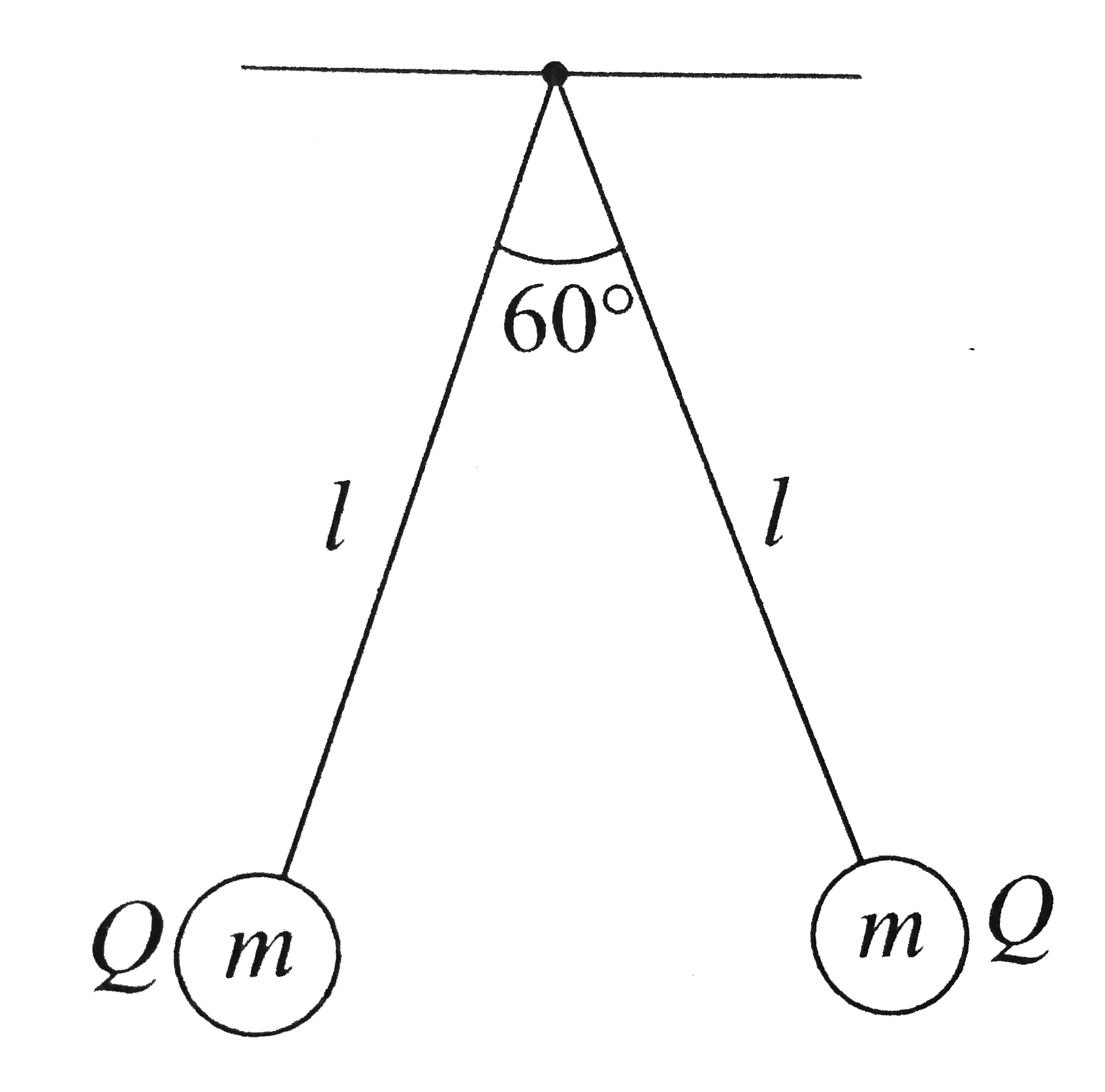
View Solution
