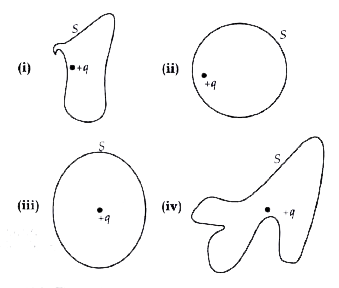Which of the following is true for electric flux through a Gaussian surface ?
It depends on magnitude of charge
Electric flux is a scalar quantity
Electric flux is independent of shape of Gaussian surface enclosing the charge
All are true
To determine which statements are true regarding electric flux through a Gaussian surface, we can analyze the situation using Gauss's Law. Here’s a step-by-step breakdown of the solution:
1. Understanding Gaussian Surface:
- A Gaussian surface is an imaginary closed surface used in Gauss's Law to calculate the electric flux due to enclosed charges.
2. Gauss's Law Statement:
- Gauss's Law states that the total electric flux (Φ) through a closed surface is equal to the total charge (Q) enclosed within that surface divided by the permittivity of free space (ε₀):
Φ=Qencϵ0
3. Analyzing the Options:
- Option 1: "It depends on the magnitude of the charge."
- This is true because the electric flux is directly proportional to the total charge enclosed.
- Option 2: "Electric flux is a scalar quantity."
- This is also true. Although the electric field is a vector, the electric flux is calculated as a dot product and results in a scalar quantity.
- Option 3: "Electric flux is independent of the shape of the Gaussian surface."
- This is true as well. The electric flux only depends on the total charge enclosed, not on the shape or size of the Gaussian surface.
- Option 4: "All are true."
- Since options 1, 2, and 3 are all true, this option is correct.
4. Conclusion:
- Therefore, the correct answer is that all the statements provided are true regarding the electric flux through a Gaussian surface.
Final Answer:
All statements regarding electric flux through a Gaussian surface are true.
---
- A Gaussian surface is an imaginary closed surface used in Gauss's Law to calculate the electric flux due to enclosed charges.
- Gauss's Law states that the total electric flux (Φ) through a closed surface is equal to the total charge (Q) enclosed within that surface divided by the permittivity of free space (ε₀):
Φ=Qencϵ0
- Option 1: "It depends on the magnitude of the charge."
- This is true because the electric flux is directly proportional to the total charge enclosed.
- Option 2: "Electric flux is a scalar quantity."
- This is also true. Although the electric field is a vector, the electric flux is calculated as a dot product and results in a scalar quantity.
- Option 3: "Electric flux is independent of the shape of the Gaussian surface."
- This is true as well. The electric flux only depends on the total charge enclosed, not on the shape or size of the Gaussian surface.
- Option 4: "All are true."
- Since options 1, 2, and 3 are all true, this option is correct.
- Therefore, the correct answer is that all the statements provided are true regarding the electric flux through a Gaussian surface.
All statements regarding electric flux through a Gaussian surface are true.
Similar Questions
Knowledge Check
The electric flux through a closed Gaussian surface depends upon
Anet charge enclosed and permittivity of the medium.Bnet charge enclosed, permittivity of the medium and the size of the Gaussian surface.Cet charge enclosed only.Dpermittivity of the medium only.The electric flux through the surface
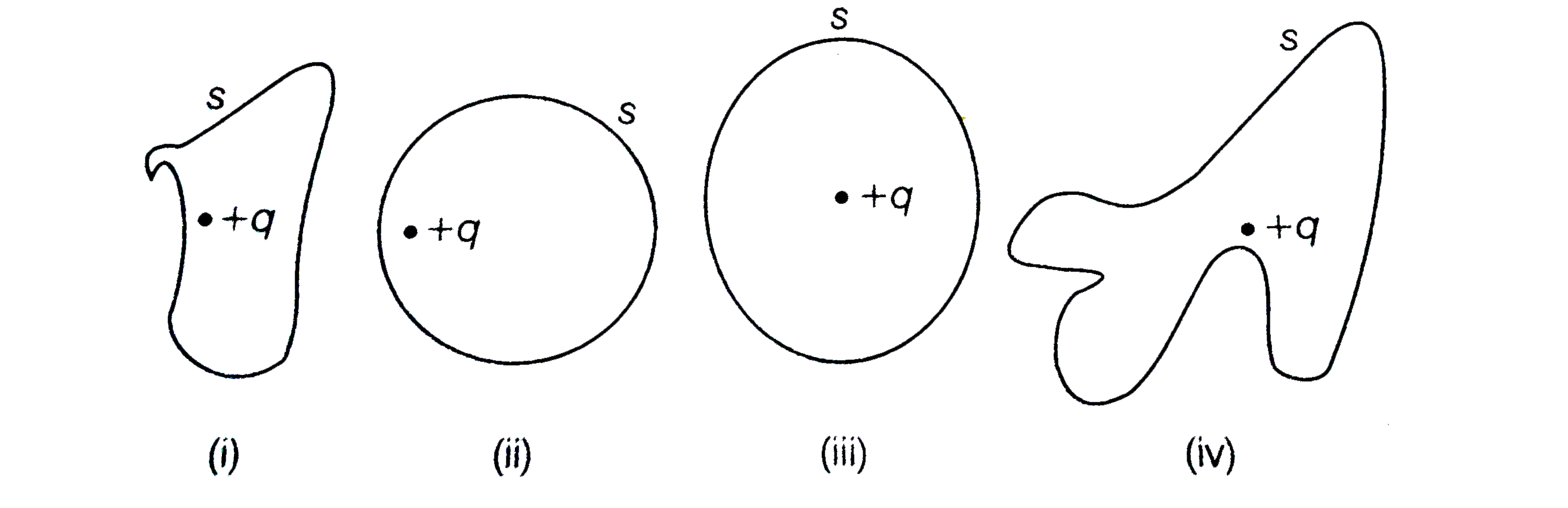 Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.
Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.The electric flux through the surface
 Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.
Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.
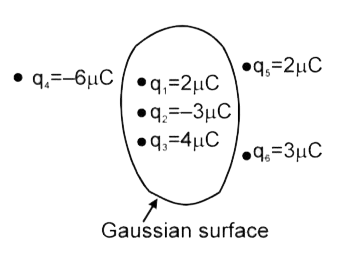
Find out flux through the given Gaussian surface.

View SolutionIf the radius of the Gaussion surface enclosing a charge q is halved, how does the electric flux through the Gaussion surface change?
View SolutionAn infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surfance of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surfce is .

View SolutionIn the situatiioni when the Gaussian surface is so chosen that there are some charges inside and some outside, then regarding the electric field at any point and the electric flux through the Gaussaina surface, which of the following is correct?
View SolutionWhich of the following law gives a relation between the electric flux through any closed surface and the charge enclosed by the surface ?
View Solution