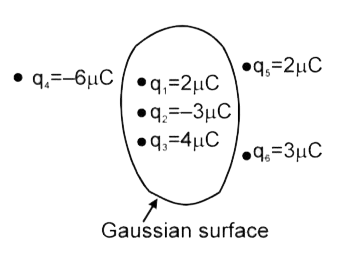
Find out flux through given gaussian surface.
Video Solution
Text Solution
ϕ=Qinε0=2μC−3μC+4μCε0=3×10−6ε0Nm2/C
|
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - SELF MISCELLANEOUS PROBLEM (Example )
15 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - SELF PRACTICE PROBLEM
27 Videos
- ELECTRONICS - SEMI CONDUCTORBOOK - MOTIONCHAPTER - ELECTRONICS - SEMI CONDUCTOREXERCISE - EXERCISE - 3
29 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
13 Videos
Similar Questions
Knowledge Check
The electric flux through a closed Gaussian surface depends upon
Anet charge enclosed and permittivity of the medium.Bnet charge enclosed, permittivity of the medium and the size of the Gaussian surface.Cet charge enclosed only.Dpermittivity of the medium only.Which of the following is true for electric-flux through a Gaussian surface ?
AIt depends on magnitude of charge enclosed by Gaussian surfaceBElectric flux is scalar quantityCElectric flux is independent of shape of Gaussian surface enclosing the chargeDAll are trueAn infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surfance of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surfce is .
 AπR2σɛ0Bπ(R−x)2σɛ0Cπ(R−x)2σɛ0Dπ(R2−x2)σɛ0
AπR2σɛ0Bπ(R−x)2σɛ0Cπ(R−x)2σɛ0Dπ(R2−x2)σɛ0
Which of the following is true for electric flux through a Gaussian surface ?
View SolutionFind out the flux through the curved surface of a hemisphere of radius R if it is placed in a uniform electric field E as shown in figure
View SolutionIf net flux through a Caussian surface is zero, then find whether the following statements are correct or not.
There are no changes inside the surface.
View SolutionFind flux through the hemispherical surface
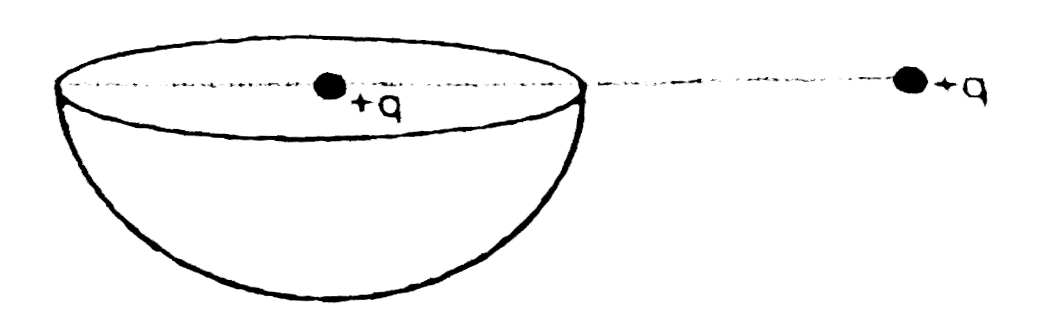
View SolutionFind flux through the hemispherical surface

View Solution
