An electron released on the axis of a positively charged ring at a large distance from the centre will
Not move
Do oscillatory motion
Do SHM
Do non-periodic motion
The correct Answer is:B
To solve the problem of an electron released on the axis of a positively charged ring at a large distance from the center, we can follow these steps:
Step 1: Understand the Electric Field Due to the Ring
At a large distance x from the center of the ring, the electric field E due to a uniformly charged ring can be expressed as:
E=k⋅Q⋅x(R2+x2)3/2
where k is Coulomb's constant, Q is the total charge of the ring, R is the radius of the ring, and x is the distance from the center of the ring along its axis.
Step 2: Analyze the Force on the Electron
The force F acting on the electron (which has charge −e) due to the electric field is given by:
F=−e⋅E
Substituting the expression for E:
F=−e⋅k⋅Q⋅x(R2+x2)3/2
The negative sign indicates that the force is directed towards the center of the ring (attraction).
Step 3: Determine the Nature of Motion
As the electron is released, it will experience a force directed towards the center of the ring. This force will cause the electron to accelerate towards the ring. As it approaches the ring, the electric field strength will change, but the force will always act towards the center.
Step 4: Identify the Type of Motion
Since the force acting on the electron is always directed towards the center, the electron will oscillate about the center of the ring. However, the relationship between the force and displacement is not linear (as it is proportional to 1x2), which means the motion will not be simple harmonic motion (SHM).
Step 5: Conclusion
The electron will undergo oscillatory motion but not SHM. The oscillation will be periodic but not simple harmonic due to the nature of the force being inversely proportional to the square of the distance.
Final Answer
The electron will undergo oscillatory motion.
---
At a large distance x from the center of the ring, the electric field E due to a uniformly charged ring can be expressed as:
E=k⋅Q⋅x(R2+x2)3/2
where k is Coulomb's constant, Q is the total charge of the ring, R is the radius of the ring, and x is the distance from the center of the ring along its axis.
The force F acting on the electron (which has charge −e) due to the electric field is given by:
F=−e⋅E
Substituting the expression for E:
F=−e⋅k⋅Q⋅x(R2+x2)3/2
The negative sign indicates that the force is directed towards the center of the ring (attraction).
As the electron is released, it will experience a force directed towards the center of the ring. This force will cause the electron to accelerate towards the ring. As it approaches the ring, the electric field strength will change, but the force will always act towards the center.
Since the force acting on the electron is always directed towards the center, the electron will oscillate about the center of the ring. However, the relationship between the force and displacement is not linear (as it is proportional to 1x2), which means the motion will not be simple harmonic motion (SHM).
The electron will undergo oscillatory motion but not SHM. The oscillation will be periodic but not simple harmonic due to the nature of the force being inversely proportional to the square of the distance.
The electron will undergo oscillatory motion.
Similar Questions
The largest magnitude the electric field on the axis of a uniformly charged ring of radius 3m is at a distance h from its centre. What is the value of h? (Take 1√2=0.7)
View SolutionAn infinite dielectric sheet having charge density σ has a hole of radius R in it. An electron is released on the axis of the hole at a distance √3R from the center. Find the speed with which it crosses the center of the hole.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
An electric dipole is kept on the axis of a uniformly charged ring at distance d from the centre of the ring. The direction of the dipole moment is along the axis. The dipole moment is p, charge of the ring is Q & radius of the ring is R. The force on the dipole is
ApQ3πε0√3R2B4pQ3πε0√3R2CpQ3πε0R2Dzero - Question 2 - Select One
There is a uniformly charged ring having radius R. An infinite line charge (charge per unit length lambda) is placed along a diameter of the ring (in gravity free space). Total charge on the ring Q=4√2λR. An electron of mass m is released from rest on the axis of the ring at a distance x=√3R from the centre.
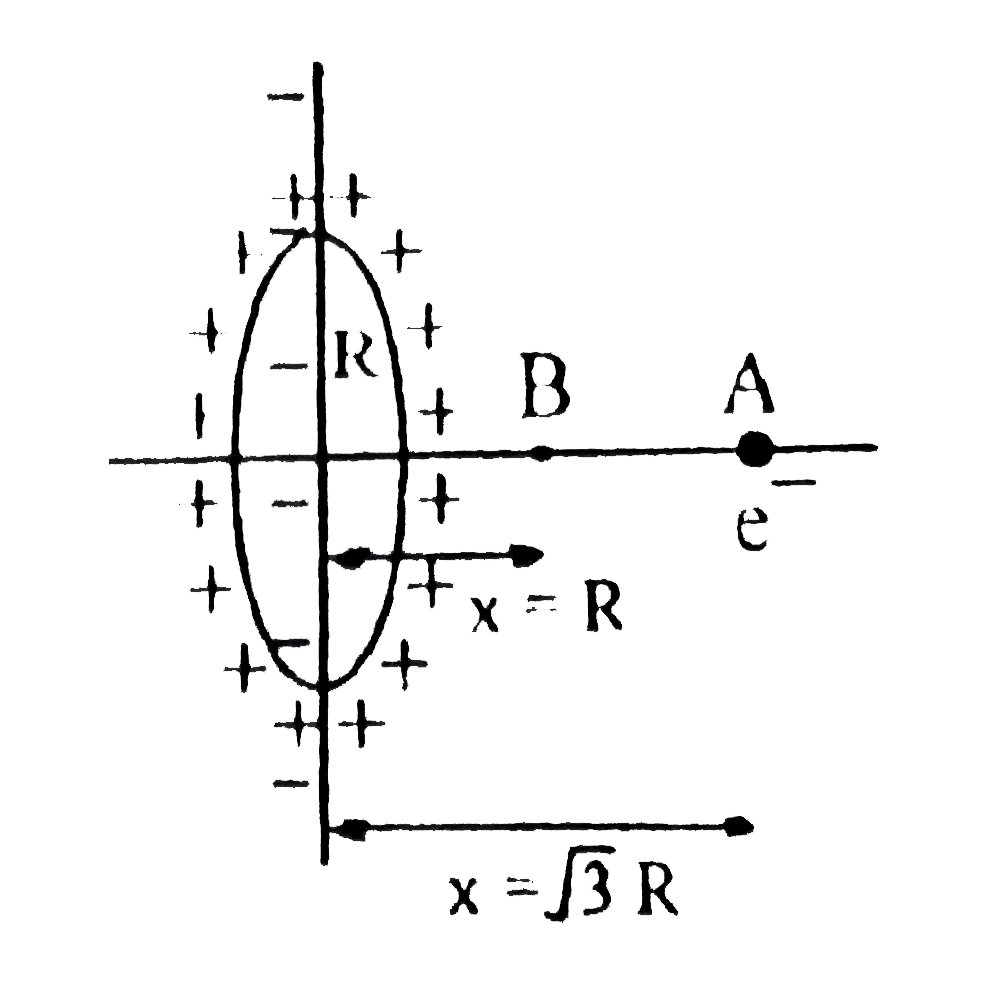
The distance from centre of ring on the axis where the net force on the electron is zero.A2RB√2RCRDnone of these - Question 3 - Select One
A ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
Akq2x(a2+x2)32B2kq2x(a2+x2)32Ckq2x(a2+x2)32Dkq22x(a2+x2)32
The largest magnitude the electric field on the axis of a uniformly charged ring of radius 3m is at a distance h from its centre. What is the value of h? (Take 1√2=0.7)
View SolutionA ring has radius 30cm and a charge of 2nC .The electric potential on the axis of the ring at a distance of 40cm from its centre will be
View SolutionA ring of radius R carries a uniformly distributed charge +Q. A point charge −q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a ismple harmonic motion along the axis of the ring.
View SolutionThere is a uniformly charged ring having radius R. An infinite line charge (charge per unit length lambda) is placed along a diameter of the ring (in gravity free space). Total charge on the ring Q=4√2λR. An electron of mass m is released from rest on the axis of the ring at a distance x=√3R from the centre.
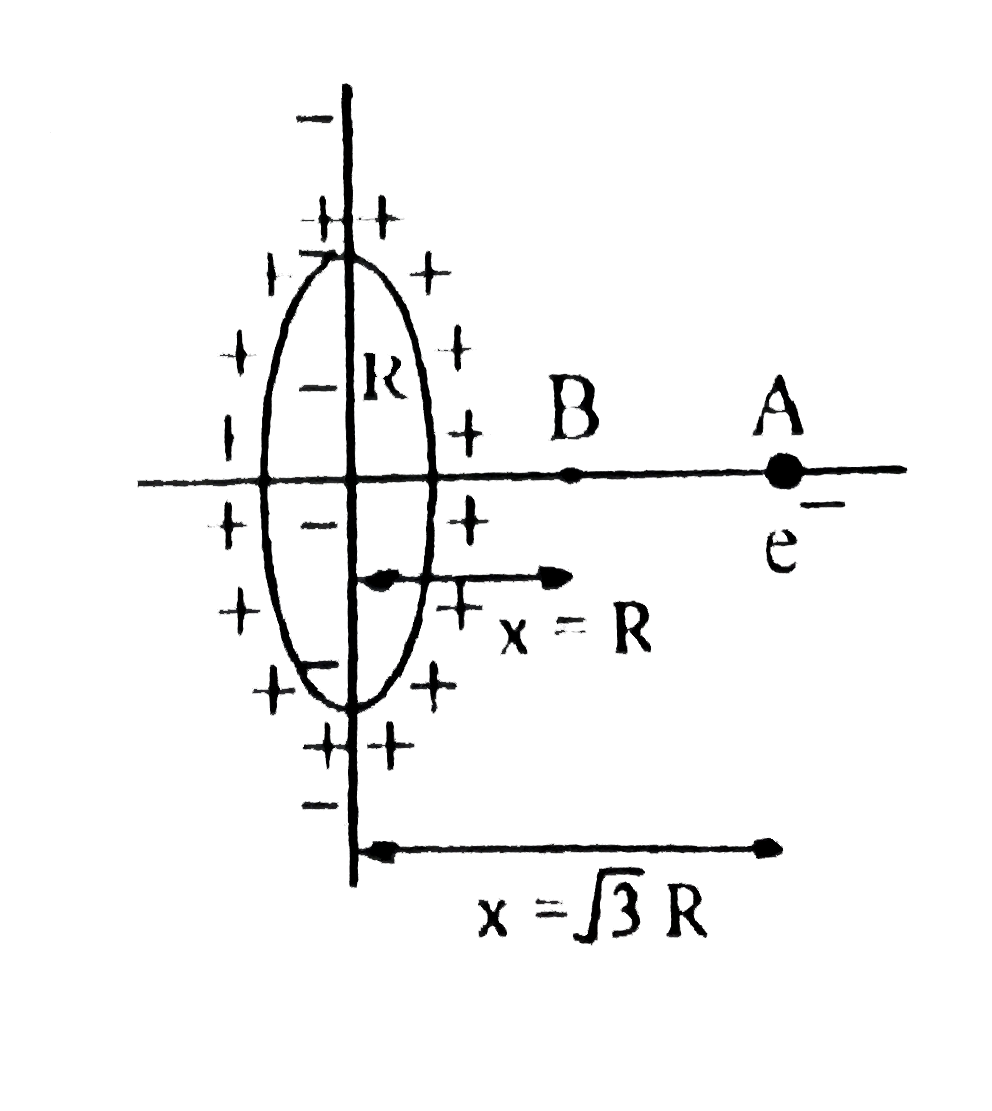
Magnitude of initial acceleration of the electron.View SolutionWhich statement is true :-
(i) A ring of radius R carries a uniformly distributed charge +Q. A point charge -q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a smiple harmonic motion along the axis of the ring.
(ii) Electrons move from a region of higher potential to that of lower potentialView Solution

