Lens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
If two lens parts obtained in (b) are joined together as shown in Fig. (c), (i) what is the net power of the combination?
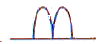
When two parts cut along section XX. are joined as shown in figure (c) (i), then
Net power =P+P=2P=2×power of original biconvex lens
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - U-LIKE SERIESCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - MULTIPLE CHOICE QUESTIONS
39 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - U-LIKE SERIESCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - FILL IN THE BLANKS
20 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - U-LIKE SERIESCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SELF ASSESSMENT TEST (SECTION B)
3 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - U-LIKE SERIESCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - SECTION B
1 Videos
Similar Questions
Lens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
If twoplanoconvex lenses fromed as a result of (a) are joined together as shown in Fig. (b), what is the net power of the combination ?
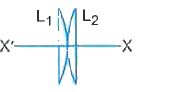
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
How is result of part (d) modified if two parts are placed together as shown in Fig. (c)(ii)?
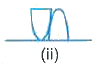
View Solution
Knowledge Check
Consider an equiconvex lens of radius of curvature R and focal length f. If f>R , the refractive index μ of the material of the lens
Ais greater than zero but less than 1.5Bis greater than 1.5 but less then 2.0Cis greater than 1.0 but less than 1.5DNone of theseIf R1 and R2 are the radii of curvature of double convex lens made of same material, the lens with more focal length is
AR1=20cm,R2=10cmBR1=R2=20cmCR1=R2=10cmDR1=R2=5cmThe radius of curvature of each surface of a lens is 40 cm. Its refractive index is 1.5. The focal length of lens will be
A40 cmB20 cmC80 cmD30 cm
Lens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
Let the given biconvex lens be divided in two equal parts, as shown in Fig. (a), along a section YY' which is perpendicular to the principal axis of lens. What is the power of each part?

View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
How is your answer modified if the given biconvex lens is divided into two parts along a section XX' along its principal axis ?
View SolutionIf R1andR2 are the radii of curvature of the spherical surfaces of a thin lens and R1>R2, then this lens can
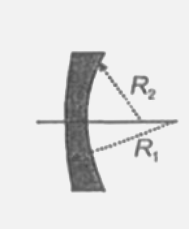
View SolutionIf R1andR2 are the radii of curvature of the spherical surfaces of a thin lens and R1>R2, then this lens can

View SolutionConsider an equiconvex lens of radius of curvature R and focal length f. If f>R , the refractive index μ of the material of the lens
View Solution
