Question

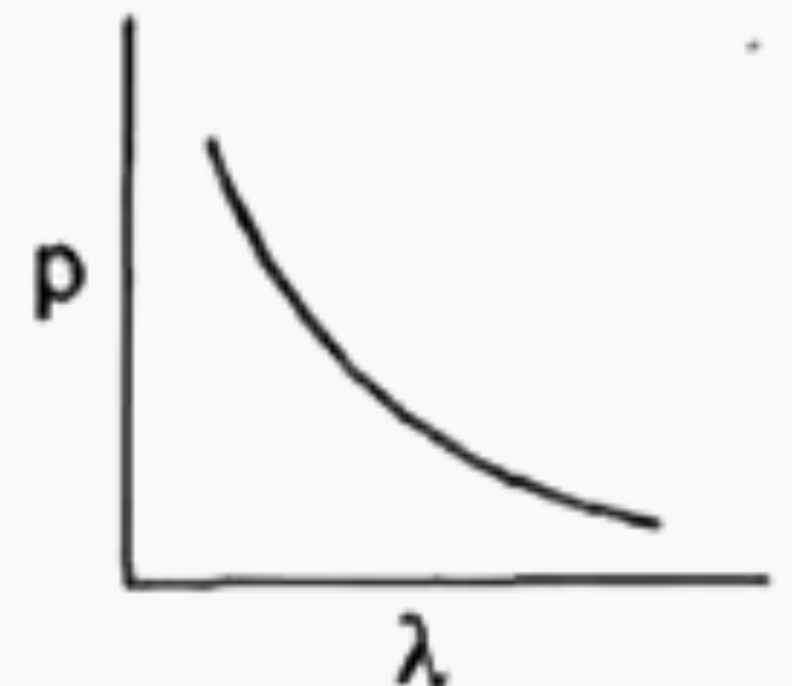
Veriation of momentum of perticle (p) with associated de-Broglie wavelength $\left(\lambda \right)$ is shown correctly by

Options

A.
B.
C.
D.

Answer

A

Explanation

To solve the problem of how the momentum $$p$$ of a particle varies with its associated de-Broglie wavelength $$\lambda$$, we can follow these steps:

Step 1: Understand the Relationship
The de-Broglie wavelength \( \lambda \) of a particle is given by the formula:
\( \lambda = \frac{h}{p} \)
where \( h \) is Planck's constant and \( p \) is the momentum of the particle.

Step 2: Rearranging the Formula
From the de-Broglie wavelength formula, we can express momentum in terms of wavelength:
\( p = \frac{h}{\lambda} \)

Step 3: Analyze the Relationship
From the equation \( p = \frac{h}{\lambda} \), we can see that:
- As the wavelength \( \lambda \) increases, the momentum \( p \) decreases.
- Conversely, as the wavelength \( \lambda \) decreases, the momentum \( p \) increases.

Step 4: Plotting the Graph
If we were to plot this relationship:
- The x-axis would represent the de-Broglie wavelength \( \lambda \).
- The y-axis would represent the momentum \( p \).

The graph would show a hyperbolic relationship, indicating that as \( \lambda \) increases, \( p \) decreases.

Step 5: Conclusion
From our analysis, we can conclude that the correct variation of momentum \( p \) with the associated de-Broglie wavelength \( \lambda \) is that momentum decreases as wavelength increases. Therefore, the correct option is the one that reflects this inverse relationship.