A voltage VAB=V0cosωt, whereV0 is a real amplitude, is applied between the points A and B in the network shown in figure. Given that
C=1ωR√3
and
L=R√3ω
(a) Calculate the total impedance between A and B.
(b) Verify that voltages of equal amplitude are developed between the point X and the points A, Y and Z.
(c) Determine the phases of these three voltages relative to VAB.
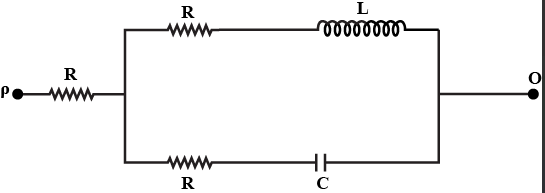
(i) 3R
(iii) (a) VAX is in same phase as VAB
(b) Phase angle between VYXandVAB=−120∘
(c) Phase angle between VZXandVAB=120∘
Topper's Solved these Questions
Similar Questions
A voltage VPQ=V0cosωt, whereV0 is a real amplitude, is applied between the points P and Q in the network shown in figure.

Given that
C=1ωR√3
and
L=R√3ω
Calculate the total impedance between P and Q.
View SolutionFind the potential difference between points A and B (VB−VA) in the network
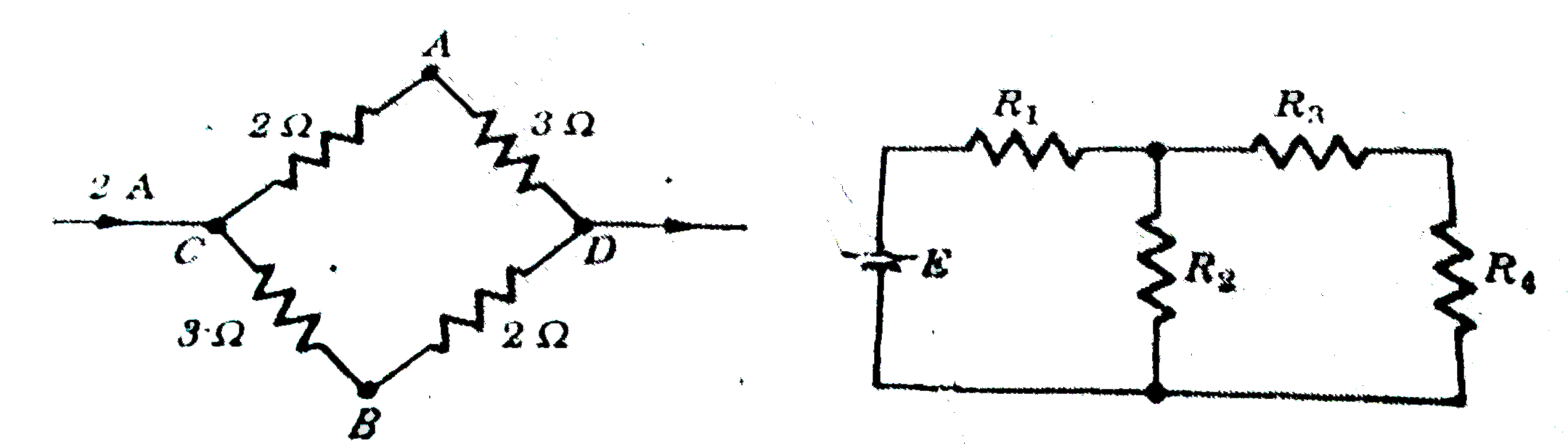
View Solution
Knowledge Check
The potential difference (VA−VB) between the point A and B in the given figure is :
 A+6VB+9VC−3VD−8V
A+6VB+9VC−3VD−8VThe potential difference (VA−VB) between the point A and B in the given figure is
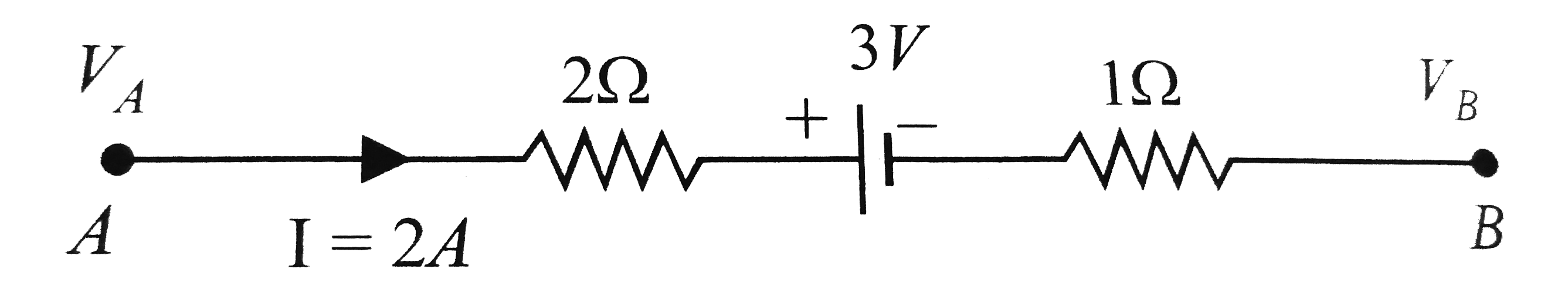 A+6VB+9VC−3VD+3V
A+6VB+9VC−3VD+3V
The potential difference (VA−VB) between the point A and B in the given figure is :

View SolutionThe potential difference (VA−VB) between the point A and B in the given figure is
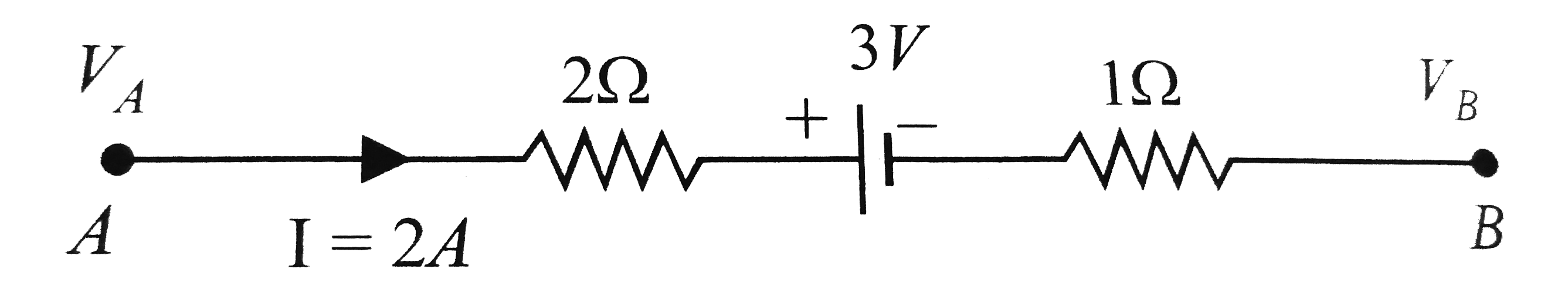
View SolutionThe potential difference (VA−VB) between the point A and B in the given figure is
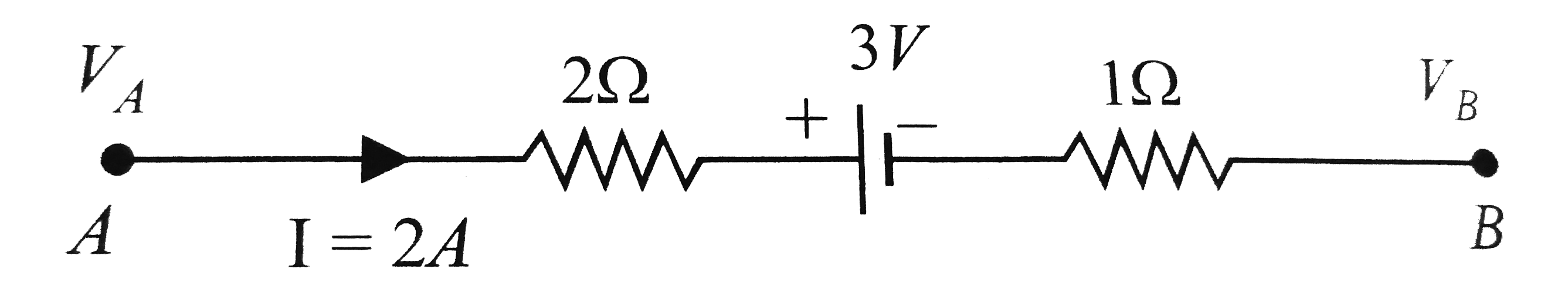
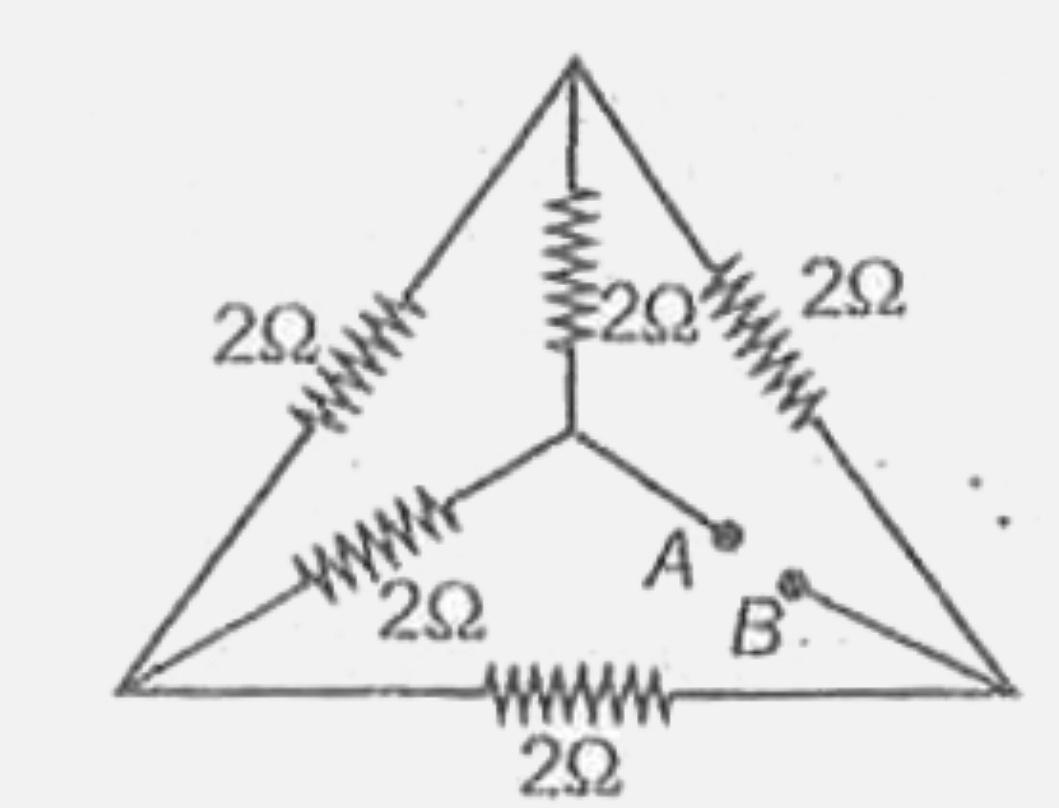
View SolutionIn the network shown in the figure, each of the resistance is equal to 2Ω . The resistance between the point A and B is
View SolutionConsider an infinte ladder network shown in figure. A voltage V is applied between the points A and B. This applied value of voltage is halved after each section.

View SolutionIn the circuit as shown in figure,
E1=2V,E2=2V,E3=1V,andR=r1=r2=r3Ω.
The potential difference between points A and B will be

View Solution
