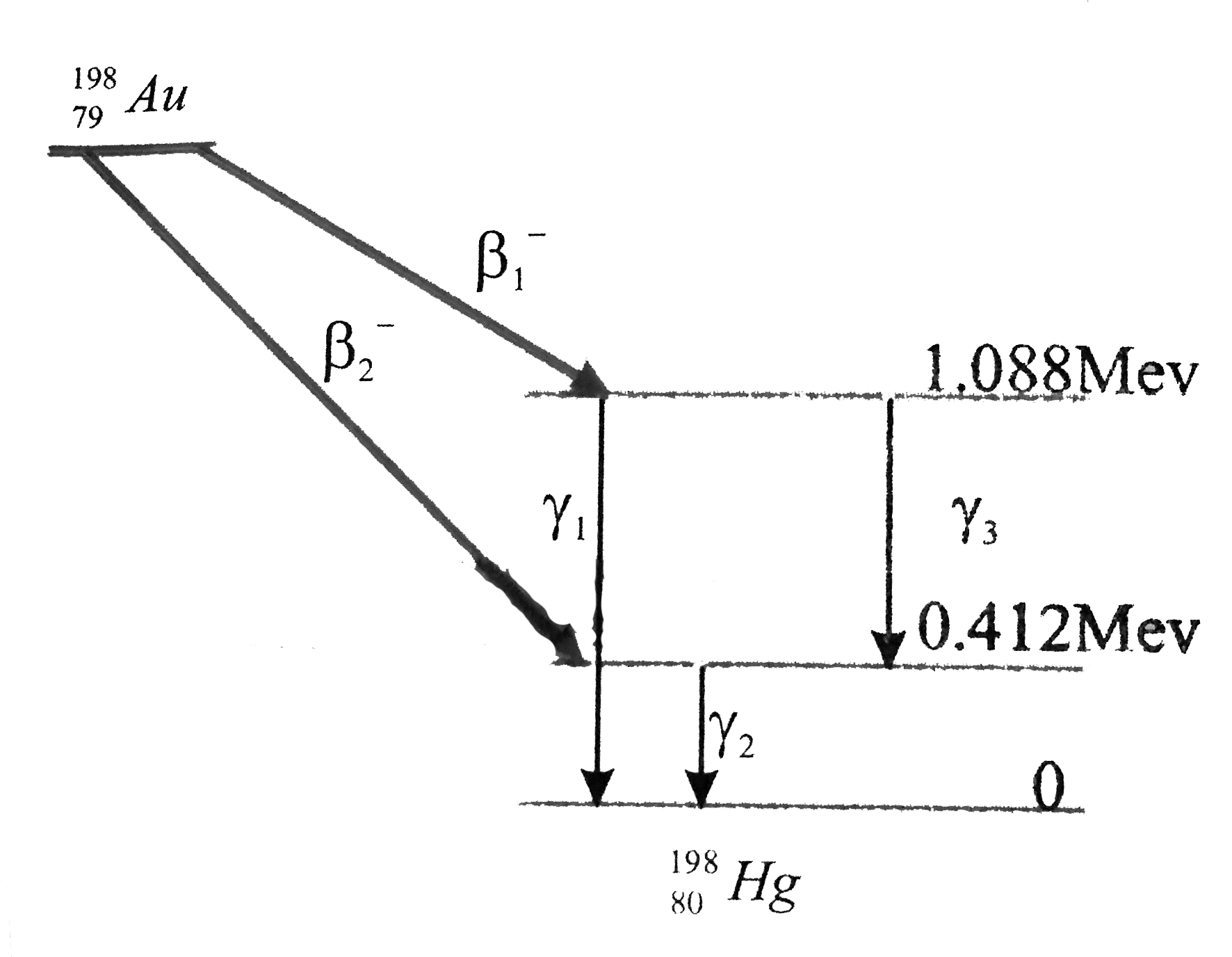
Calculate the kinetic energy of β-particles and the radiation frequencies corresponding to the γ-decays shown in figure.
Given, mass of .12Mg27 atom =26.991425 amu and mass of .13Al27 atom = 26.990080 amu

Energy of photon v1,hv1=E3−E2h=(1.015−0.834)MeV6.62×10−34Js
0.181×1.6×10−13J(6.62×10−34Js)=4.37×1019s−1
Energy of photon v2,v2=E3−E1h=(1.015−0)MeV6.62×10−34Js=2.45×1020s−1
Energy of photon v3,v3=E3−E1h=(0.834−0)MeV6.62×10−34=2.0×1020s−1
Now emission of β−1 particle is given by 12Mg27→13AI27+β−+v2+Q
Q=[m(12Mg27)−m(13AI27)−E(v2)
=[26.991425−26.990080]u−(E3−E1)MeV
=0.001345×931−1.015MeV
∴ K.E of β−2 particle is given by 12Mg27→13AI27+β−2+v3+Q
={[26.991425−26.990080]931−0.34}MeV
=0.418 MeV
Topper's Solved these Questions
- NUCLEIBOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - EXERCISE
20 Videos
- NUCLEIBOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-A)
39 Videos
- NUCLEIBOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - Assignment Section J (Aakash Challengers Questions)
4 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section J (Aakash Challengers Questions)
5 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)
13 Videos
Similar Questions
Knowledge Check
Calculate the total energy released during a fission reaction .
The resulting fission fragements are unstable hence, decay into stable and products and by sucessive emission of β-particles . Take mass of neutron = 1.0087 amu , mass of =236.0526 amu, mass of =97.9054 amu and mass of =135.9170 amu.A198 MeVB220 MeVC185 MeVD230 MeV
Calculate the binding energy of the deuteron, which consistss of a proton and a neutron, given that the atomic mass of the deuteron is 2.014102 amu,. Take mass of proton (mp)=1.007825 amu, mass of a neutron (mn)=1.008665 amu and 1amu=931.5 MeV
View SolutionWhen Lithium is bombarded by 10 MeV deutrons, neutrons are observed to emerge at right angle to the direction of incident beam . Calculate the energy of these neutrons and angle of recoil of the associated Beryllium atom.
Given Mass of .0n1=1.00893 amu
Mass of Li7=7.01784 amu
Mass of H2=2.01472 amu
Mass of Be8=8.00176 amu
View SolutionCalculate the maximum kinetic energy of the bera particle emitted in the following decay scheme:
^12N rarr 12C∗+e++v
^12C rarr ^12C+γ(4.43MeV).
The atomic mass of 12Nis12.018612u.
View SolutionCalculate the nuclear binding energy of an alpha particle from the following data.
Mass of 11H atom = 1.007825 amu
Mass of neutron = 1.008665 amu
Mass of 24He atom = 4.00260 amu
View SolutionFind the binding energy and the binding energy pernucleon of the nucleus of .168O. Given atomic mass of .168O(m)=15.994915 amu, mass of proton (mp)=1.007823 amu, mass of a neutron (mn)=1.008665 amu and 1 amu =931.5 MeV.
View SolutionThe nuclear mass of 13Al26 is 26.9815 amu. Find its nuclear density.
View SolutionCalculate the binding energy of 63Li assuming the mass of 63Li atoms as 6.01512 amu.
View Solution