There are four rods A, B, C and D of same length L but different linear mass density d, 2d, 3d & 4d respectively. These are joined to form a square frame with sides C & D along x & y axis of coordinate axes respectively. Find coordinate of centre of mass of structure. ?
To find the coordinates of the center of mass of the square frame formed by the four rods A, B, C, and D, we will follow these steps:
Step 1: Identify the coordinates of the center of mass for each rod.
- Rod A: Positioned along the x-axis from (0, 0) to (L, 0). The center of mass (CM) is at (L2,0).
- Rod B: Positioned along the y-axis from (0, 0) to (0, L). The center of mass is at (0,L2).
- Rod C: Positioned along the x-axis from (0, L) to (L, L). The center of mass is at (L2,L).
- Rod D: Positioned along the y-axis from (L, 0) to (L, L). The center of mass is at (L,L2).
Step 2: Calculate the mass of each rod.
The mass of each rod can be calculated using the formula:
Mass=Linear Mass Density×Length
- Rod A: Mass mA=d⋅L
- Rod B: Mass mB=2d⋅L
- Rod C: Mass mC=3d⋅L
- Rod D: Mass mD=4d⋅L
Step 3: Calculate the total mass of the structure.
Total Mass=mA+mB+mC+mD=dL+2dL+3dL+4dL=10dL
Step 4: Calculate the x-coordinate of the center of mass.
Using the formula for the x-coordinate of the center of mass:
xcm=1M∑(mi⋅xi)
Substituting the values:
xcm=110dL(mA⋅L2+mB⋅0+mC⋅L2+mD⋅L)
=110dL((dL)⋅L2+(2dL)⋅0+(3dL)⋅L2+(4dL)⋅L)
=110dL(dL22+0+3dL22+4dL2)
=110dL(4dL22+4dL2)
=110dL(2dL2+4dL2)=6dL210dL=3L5
Step 5: Calculate the y-coordinate of the center of mass.
Using the formula for the y-coordinate of the center of mass:
ycm=1M∑(mi⋅yi)
Substituting the values:
ycm=110dL(mA⋅0+mB⋅L2+mC⋅L+mD⋅L2)
=110dL(0+(2dL)⋅L2+(3dL)⋅L+(4dL)⋅L2)
=110dL(0+dL2+3dL2+2dL2)
=110dL(6dL2)=6L10=3L5
Final Result:
The coordinates of the center of mass of the structure are:
(3L5,3L5)
- Rod A: Positioned along the x-axis from (0, 0) to (L, 0). The center of mass (CM) is at (L2,0).
- Rod B: Positioned along the y-axis from (0, 0) to (0, L). The center of mass is at (0,L2).
- Rod C: Positioned along the x-axis from (0, L) to (L, L). The center of mass is at (L2,L).
- Rod D: Positioned along the y-axis from (L, 0) to (L, L). The center of mass is at (L,L2).
The mass of each rod can be calculated using the formula:
Mass=Linear Mass Density×Length
- Rod A: Mass mA=d⋅L
- Rod B: Mass mB=2d⋅L
- Rod C: Mass mC=3d⋅L
- Rod D: Mass mD=4d⋅L
Total Mass=mA+mB+mC+mD=dL+2dL+3dL+4dL=10dL
Using the formula for the x-coordinate of the center of mass:
xcm=1M∑(mi⋅xi)
Substituting the values:
xcm=110dL(mA⋅L2+mB⋅0+mC⋅L2+mD⋅L)
=110dL((dL)⋅L2+(2dL)⋅0+(3dL)⋅L2+(4dL)⋅L)
=110dL(dL22+0+3dL22+4dL2)
=110dL(4dL22+4dL2)
=110dL(2dL2+4dL2)=6dL210dL=3L5
Using the formula for the y-coordinate of the center of mass:
ycm=1M∑(mi⋅yi)
Substituting the values:
ycm=110dL(mA⋅0+mB⋅L2+mC⋅L+mD⋅L2)
=110dL(0+(2dL)⋅L2+(3dL)⋅L+(4dL)⋅L2)
=110dL(0+dL2+3dL2+2dL2)
=110dL(6dL2)=6L10=3L5
The coordinates of the center of mass of the structure are:
(3L5,3L5)
Similar Questions
Knowledge Check
- Question 1 - Select One
In the arrangement as shown, A and B arc two cylinders each of length L and density d1 and d2(d1<d2) respectively. They are joined together and submerged in the liquid of density d with length L/2 of A outside the liquid. If the difference in densities of two cylinders is equal to density of the liquid, find d1.
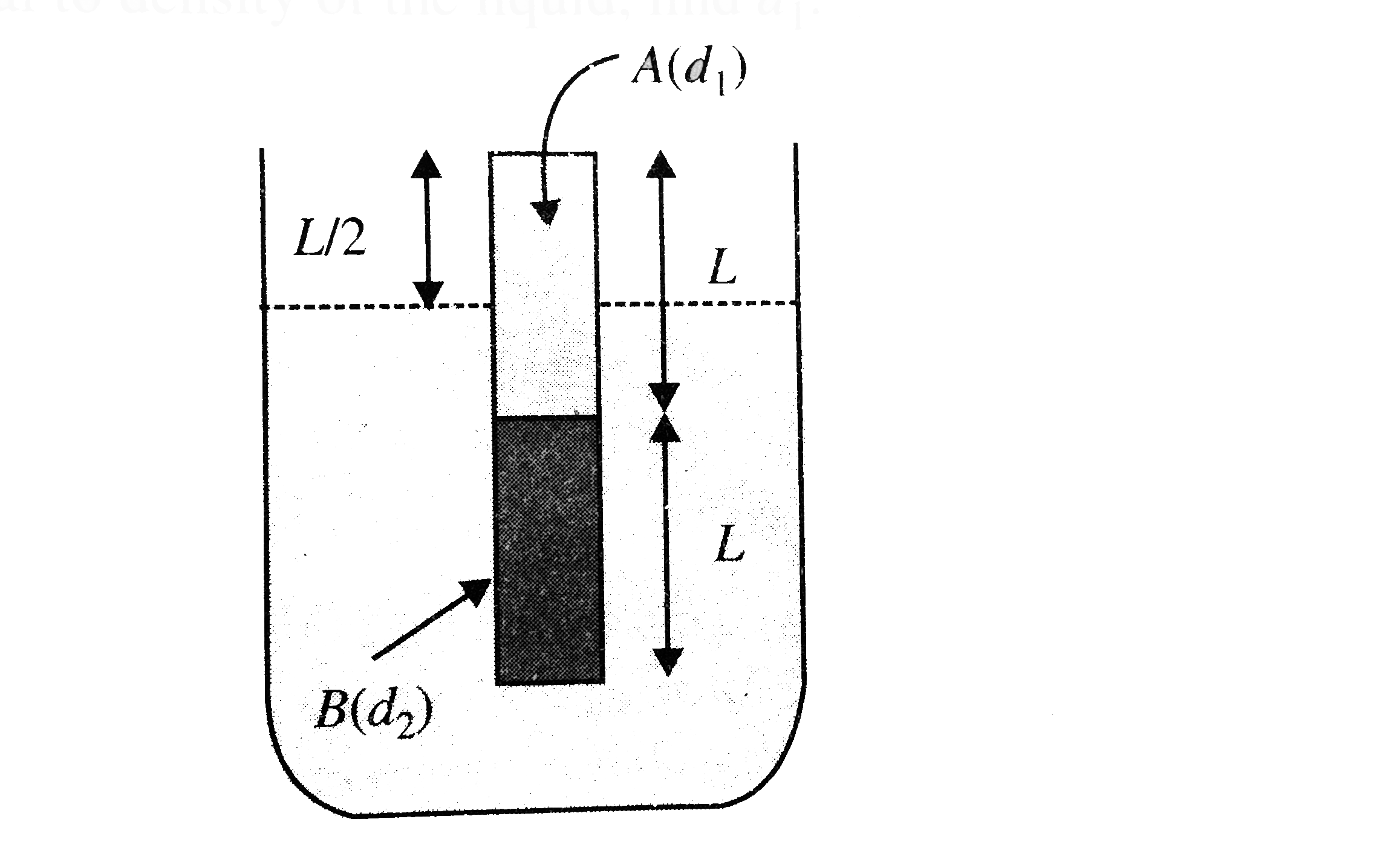 A54dBd4C34dDd2
A54dBd4C34dDd2 - Question 2 - Select One
Four particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
A(0.5,0.3)B(0.4,0.3)C(0.5,0.8)D(0.7,0.3) - Question 3 - Select One
Four bodies of masses 1,2,3,4kg respectively are placed at the comers of a square of side a. Coordinates of centre of mass are (take 1kg at the origin,2kg on X-axis and 4kg on Y-axis)
A(7a10,a2)B(a2,7a10)C(a2,3a10)D(7a10,3a2)
A ,B and C are the points (2,0),(5,0)and(5,3) respectively. Find coordinates of D such that ABCD is a square.
View SolutionFour particles A,B,CandD of masses m,2m,3mand4m respectively are placed at corners of a square of side x as shown in Fig.

Locate the centre of mass.View SolutionABCD is a square having length of a side 20 units. Taking the centre of the square as the origin and xandy axes parallel to AB and AD respectively, find the coordinates of A, B, C and D.
View SolutionABCD is a parallelogram. If the coordinates of A, B, C are (2,3), (1,4)and (0,−2) respectively, find the coordinates of D.
View SolutionThe position vectors of four points A, B, C, D lying in a plane are a, b, c, d respectively. They satisfy the relation |a−d|=|b−d|=|c−d| then the point D is
View Solution


