A battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω 22. Determine the equivalent resistance of the network and the current along each edge of the cube.
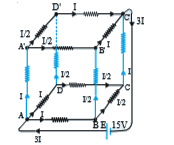
The network is not reducible to a simple series and parallel combinations of resistors. There is, however, a clear symmetry in the problem which we can exploit to obtain the equivalent resistance of the network. The paths AA., AD and AB are obviously symmetrically placed in the network. Thus, the current in each must be the same, say, I. Further, at the corners A., B and D, the incoming current I must split equally into the two outgoing branches. In this manner, the current in all the 12 edges of the cube are easily written down in terms of I, using Kirchhoff.s first rule and the symmetry in the problem. Next take a closed loop, say, ABCC.EA, and apply Kirchhoff.s second rule:
−IR−(1/2)IR−IR+E = 0 where R is the resistance of each edge and E the emf of battery. Thus, E =52IR
The equivalent resistance Ras of the network is
Req=E3I=56R
For R = 6Ω,Req = 5Ω and for E = 15 V
the total current = 31 ) in the network is
3I = 15/5= 3 A, i.e., I = 1A
The current flowing in each edge can now be read off from the figure.
Similar Questions
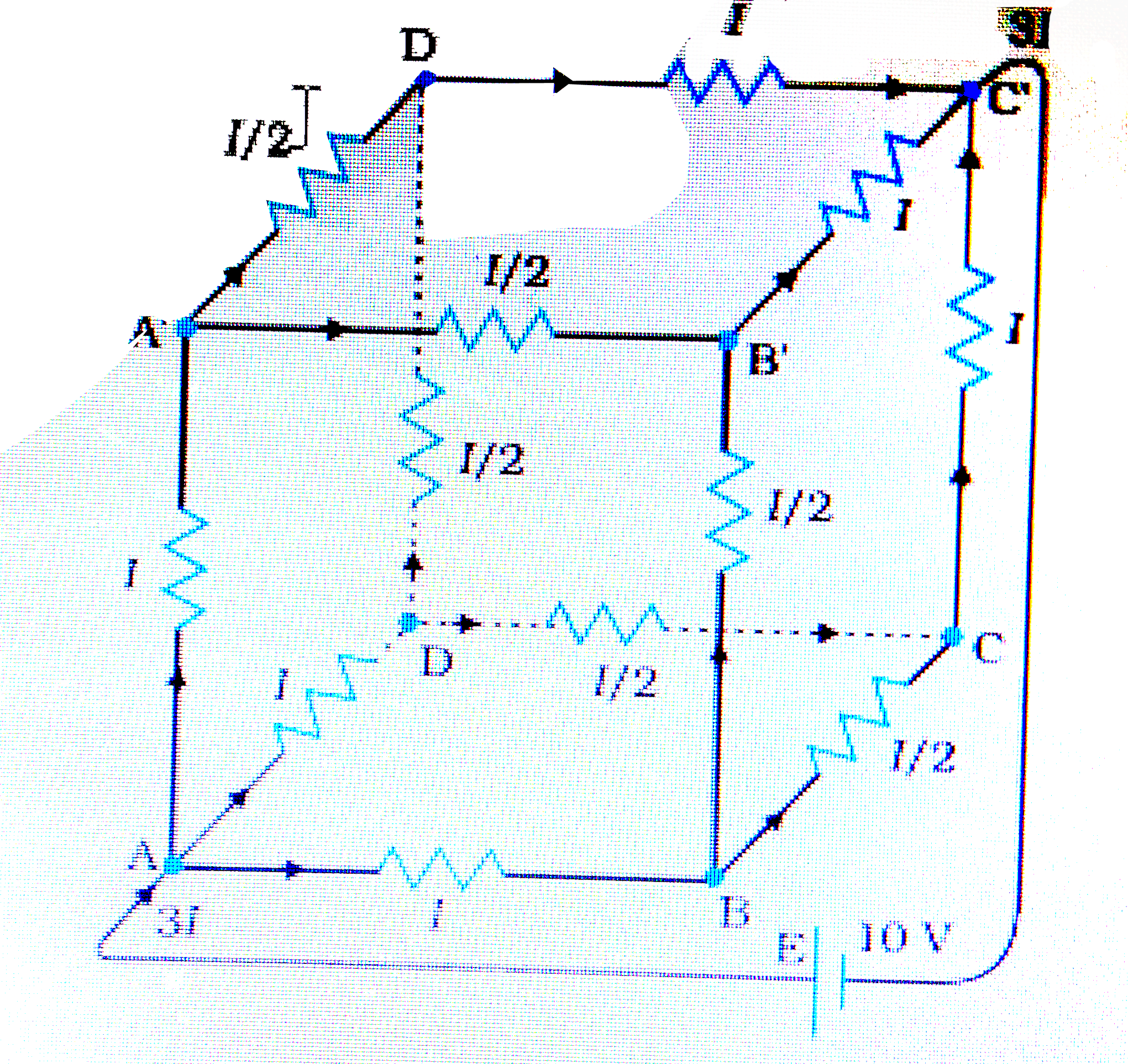
Battery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω (Fig. 3.23). Determine the equivalent resistance of the network and the current along each edge of the cube.
 View Solution
View SolutionA battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω 22. Determine the equivalent resistance of the network and the current along each edge of the cube.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Twelve wires, each of resistance 1Ω are connected to form a skeleton cube. Battery of 10V and neglibible internal resistance is connected across diagonally opposite corners of the cube. Determine the equivalent resistance of the network and current supplied by the battery.
A56Ω and 12AB65Ω and 12 AC56Ω 4AD65Ω and 4A - Question 2 - Select One
Three resistors each of 4Ω are connected together to form a network. The equivalent resistance of the network cannot be
A1.33ΩB3.0ΩC6.0ΩD12.0Ω - Question 3 - Select One
The figure shows a network of resistor each having value 12Ω. Find the equivalent resistance between points A and B.
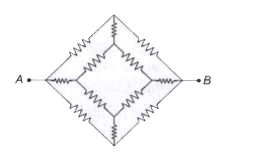 A9ΩB125ΩC8ΩD113Ω
A9ΩB125ΩC8ΩD113Ω
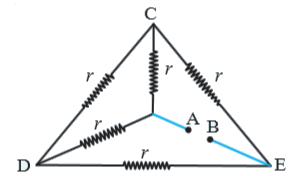
In the adjoining network of resistors each is of resistance rΩ. Find the equivalent resistance between A and B.
 View Solution
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance in 1 second?
View SolutionThe terminals of a battery of emf 3 V and internal resistance 2.5Ω are joined to the diagonally opposite corners of a cubical skeleton frame of 12 wires, each of resistance 3Ω. Find the current in the battery.
View SolutionIn the given network of resistors, each of resistance R, calculate the equivalent resistance between the junctions A and E
 View Solution
View SolutionIn the adjoining network of resistors, each is of resistance r ohm, the equivalent resistance between points A and B is–
 View Solution
View Solution

