Calculate the self inductance per unit length of a current loop formed by joining the ends of two long parallel wires of radius r separated by a distance d between their axes, neglecting the end effects and magnetic flux within the wires.

Text Solution

Verified by Experts

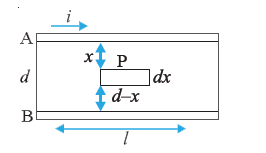
Let A and B are the two long parallel wires as shown which are formed to form a current loop. The two wires would obviously be carrying equal currents in opposite direction.Consider a space length 1 and thickness dx as shown in figure.The magnetic flux through the area 1 dx due to the currents in the two wires is dphi = Bldx where B is the intensity of magnetic field due to current carrying wires at a distance x from A. $B = \frac{μ_{0}}{4 π} \frac{2 i}{x} + \frac{μ_{0}}{4 π} . \frac{2 i}{d - x}$
$d ϕ = B l d x = \frac{μ_{0} i}{2 π} (\frac{1}{x} + \frac{1}{d - x}) l d x$ $B = \frac{μ_{0}}{4 π} \frac{2 i}{x} + \frac{μ_{0}}{4 π} . \frac{2 i}{d - x}$
$d ϕ = B l d x = \frac{μ_{0} i}{2 π} (\frac{1}{x} + \frac{1}{d - x}) l d x$
theretore $ϕ = \int_{r}^{d - r} μ_{0} i \frac{)}{2 π} (\frac{1}{x} + \frac{1}{d - x}) l d x$
$μ_{0} i \frac{l}{2 π} {[{log}_{e} x - {log}_{e} (d - x)]}_{r}^{d - r} = μ_{0} i l \frac{)}{r} {log}_{_} (e) \frac{d - r}{r}$
Magnetic flux linked with unit length of the loop = $\frac{μ_{0} i}{r} \frac{{log}_{e} (d - r)}{r}$
But phi = Li where L is self-inductancetherefore $L = \frac{μ_{0}}{r} {log}_{e} (\frac{d - r}{r})$

Updated on:21/07/2023